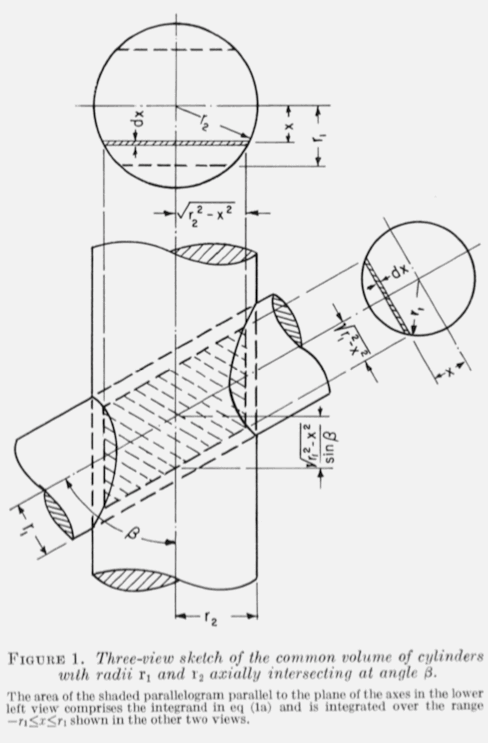
Consider two cylinders as illustrated above (Hubbell 1965) where the cylinders have radii 
and 
with 
,
the larger cylinder is oriented along the 
-axis, and where the axes of the two cylinders intersecting
at an angle 
. Then the volume of the region of intersection is given
by
 |  |  |
(1)
|
 |  |  |
(2)
|
 |  | ![(8r_2^3)/(sinbeta)[(1+k^2)E(k)-(1-k^2)K(k)]](/images/equations/Cylinder-CylinderIntersection/Inline14.svg) |
(3)
|
 |  |  |
(4)
|
 |  |  |
(5)
|
where
 |
(6)
|
Here, 
and 
are complete elliptic integrals
of the first and second
kinds, respectively, 
is a hypergeometric
function, and 
is a binomial coefficient.
The intersection of two (or three) right cylinders of equal radii intersecting at right angles is known as the Steinmetz solid.
