The fundamental group of an arcwise-connected set
is the group formed by the sets of equivalence
classes of the set of all loops, i.e., paths with initial
and final points at a given basepoint
, under the equivalence
relation of homotopy. The identity
element of this group is the set of all paths homotopic
to the degenerate path consisting of the point
. The fundamental groups of homeomorphic
spaces are isomorphic. In fact, the fundamental group
only depends on the homotopy type of
. The fundamental group of a topological
space was introduced by Poincaré (Munkres 1993, p. 1).
The following is a table of the fundamental group for some common spaces , where
denotes the fundamental group,
is the first integral homology group,
denotes the group
direct product,
denotes the free product,
denotes the ring of integers,
and
is the cyclic group of order
.
| space ( | symbol | ||
| circle | |||
| complex projective space | 0 | 0 | |
| figure eight | |||
| Klein bottle | |||
| real projective plane | |||
| sphere | 0 | 0 |
The group product
of loop
and loop
is given by the path of
followed by the path of
. The identity element is represented by the constant path,
and the inverse of
is given by traversing
in the opposite direction. The fundamental group is independent
of the choice of basepoint because any loop through
is homotopic to a loop through
any other point
.
So it makes sense to say the "fundamental group of
."
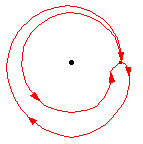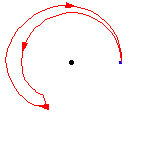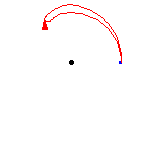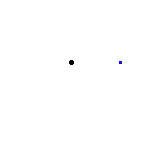
The diagram above shows that a loop followed by the opposite loop is homotopic to the constant loop, i.e., the identity. That is, it starts by traversing the path
,
and then turns around and goes the other way,
. The composition is deformed, or homotoped, to the constant
path, along the original path
.
A space with a trivial fundamental group (i.e., every loop is homotopic to the constant loop), is called simply connected. For instance,
any contractible space, like Euclidean
space, is simply connected. The sphere is simply
connected, but not contractible. By definition,
the universal cover is simply connected, and loops in
lift to paths in
. The lifted paths in the universal cover define the deck
transformations, which form a group isomorphic to the
fundamental group.
The underlying set of the fundamental group of is the set of based homotopy
classes from the circle to
, denoted
. For general spaces
and
, there is no natural group structure on
, but when there is,
is called a co-H-space. Besides
the circle, every sphere
is a co-H-space,
defining the homotopy groups. In general, the fundamental
group is non-Abelian. However, the higher homotopy
groups are Abelian. In some special cases, the fundamental group is Abelian.
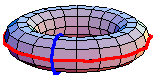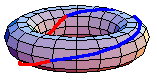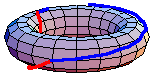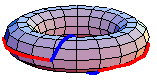
For example, the animation above shows that
in the torus. The red path
goes before the blue path. The animation is a homotopy between the loop that goes
around the inside first and the loop that goes around the outside first.
Since the first integral homology of
is also represented by loops, which are the only one-dimensional
objects with no boundary, there is a group homomorphism
which is surjective. In fact, the group kernel of
is the commutator subgroup and
is called Abelianization.
The fundamental group of can be computed using van
Kampen's theorem, when
can be written as a union
of spaces whose fundamental groups are known.
When
is a continuous map, then the fundamental group pushes forward. That is, there is
a map
defined by taking the image of loops from
. The pushforward map is natural, i.e.,
whenever the composition of two
maps is defined.