A Cayley graph associated with 
, where 
is a group and 
is a connection set
that excludes the identity element, is the directed graph having one vertex
for each group element and directed
edges 
whenever 
.
The Cayley graph may depend on the choice of connection
set. Its underlying undirected graph is connected iff 
generates 
(i.e., the set 
is a set of group
generators of 
).
Care is needed since the term "Cayley graph" is also used when 
is implicitly understood to be a set
of group generators for the group,
in which case the underlying undirected graph
is always connected (but in general, still dependent
on the choice of group generators). This sort
of Cayley graph of a group 
may be computed in the Wolfram
Language using CayleyGraph[G],
where the group generators used are those returned
by GroupGenerators[G].
To complicate matters further, undirected versions of proper directed Cayley graphs are also known as Cayley graphs.
An undirected Cayley graph of a particular generating set of the alternating
group 
is sometimes known as an alternating
group graph. For 
,
the usual generating sets give undirected
Cayley graphs of the cyclic group 
and the dihedral group 
that are the cycle
graph 
and the prism graph 
, respectively. Other classes of graphs
that are Cayley graphs are circulant graphs (connected if requiring a generating
set; possibly disconnected if not), cube-connected cycle graphs 
for 
, Hamming graphs, and
hypercube graphs.
A directed Cayley graph has the same outdegree and indegree at each vertex,
both equal to the cardinal
number 
of the connection set. A (directed
or undirected) Cayley graph is always vertex-transitive,
but the converse need not hold. However, a large fraction of small vertex-transitive
graphs are Cayley graphs (McKay and Royle 1990).
Holt and Royle (2020) constructed the not-necessarily-connected simple undirected vertex-transitive
graphs on at most 47 vertices, including their
Cayley or non-Cayley designations. Their transitive
group catalogue was obtained by two independent computations. The numbers of
not-necessarily-connected simple undirected
Cayley graphs, counted up to graph isomorphism,
on 
, 2, ... nodes
are 1, 2, 2, 4, 3, 8, 4, 14, 9, 20, 8, 74, ... (OEIS A185959;
McKay and Royle 1990, McKay and Praeger 1994, Holt and Royle 2020), and the numbers
of nodes on which non-Cayley vertex-transitive
graphs exist are 10, 15, 16, 18, 20, 24, 26, 28, 30, ....
The Petersen graph 
is a smallest simple undirected vertex-transitive non-Cayley graph,
having 10 vertices (McKay and Praeger 1994). Two
copies of 
form a smallest disconnected simple undirected vertex-transitive
non-Cayley graph.
For a finite permutation group, start with a connection set 
that does not contain the identity
permutation, and form the subgroup 
generated by 
. Its vertices are all the
permutations in 
, but its directed edges use
only 
.
With the convention above, an edge from 
to 
is present when 
,
equivalently when 
for some 
. Replacing the connection
set by all nonidentity elements of 
would instead give a complete
graph after forgetting directions.
The finite groups admitting a Cayley graph that is connected and whose underlying
undirected graph is planar
are, up to isomorphism, 
, 
,
, 
, 
, 
,
, 
, 
, and 
(Maschke 1896). Here, 
for the cyclic groups
and 
for the dihedral
groups. The finite hypothesis is essential. For example,
the infinite groups 
and 
also have planar Cayley
graphs.
The following table lists some graphs that are undirected versions of Cayley graphs generated by small numbers of small permutations.
| graph | generators |
16-cell graph  |   1,2,4,3 ,  2,1,3,4 ,  2,1,4,3 ,  3,4,1,2 ,  3,4,2,1  |
circulant
graph  |   1,2,3,5,4 ,  1,2,4,3,5 ,  2,1,3,5,4 ,  2,1,5,4,3  |
complete
bipartite graph  |   1,2,4,3 ,  2,1,3,4 ,  3,4,2,1  |
  1,2,4,3 ,  2,1,3,4 ,  3,4,1,2 ,  4,3,2,1  | |
  1,2,4,5,6,3 ,  2,1,4,5,6,3  | |
complete graph  |   1,3,2 ,  2,1,3 ,  2,3,1 ,  3,2,1  |
  1,2,4,3 ,  1,3,2,4 ,  1,3,4,2 ,  1,4,3,2  | |
  1,2,4,3 ,  1,3,2,4 ,  1,3,4,2 ,  1,4,2,3 ,  1,4,3,2  | |
| cubical graph |   1,2,4,3 ,  3,4,2,1  |
  1,2,4,3 ,  2,1,3,4 ,  3,4,1,2  | |
  1,2,3,5,4 ,  1,4,5,3,2  | |
cubic
symmetric graph  |   1,2,4,3 ,  1,3,2,4 ,  3,2,1,4  |
  1,2,3,4,6,5 ,  2,5,4,6,3,1  | |
cubic symmetric graph  |   1,3,2,5,4 ,  2,1,4,3,5 ,  4,5,3,1,2  |
| cubic vertex-transitive graph Ct19 |   1,2,3,4,6,5 ,  1,2,4,3,6,5 ,  5,6,3,4,1,2  |
| cubic vertex-transitive graph Ct23 |   1,2,3,4,6,5 ,  2,3,1,5,6,4  |
| cubic vertex-transitive graph Ct28 |   1,3,2,5,4 ,  2,3,4,1,5  |
| cubic vertex-transitive graph Ct37 |   1,2,4,3 ,  1,3,2,4 , 3,4,1,2  |
| cubic vertex-transitive graph Ct38 |   1,2,3,4,5,7,6 ,  2,3,1,6,7,4,5  |
| cubic vertex-transitive graph Ct41 |   1,2,4,3 ,  1,3,2,4 , 2,1,4,3  |
| cubic vertex-transitive graph Ct42 |   1,2,3,4,5,7,6 ,  2,3,4,1,6,5,7  |
| cuboctahedral graph |   1,3,4,2 ,  2,3,1,4  |
  1,3,4,2 ,  1,4,2,3 ,  2,3,1,4  | |
  1,3,4,2 ,  1,4,2,3 ,  2,3,1,4 ,  3,1,2,4  | |
  1,2,4,5,3 ,  1,3,4,2,5  | |
| 5-cycle graph |   2,3,4,5,1 ,  5,1,2,3,4  |
| 6-cycle graph |   1,3,2 ,  2,1,3  |
  1,2,4,3 ,  1,3,2,4  | |
  1,2,3,5,4 ,  1,2,4,3,5  | |
| 8-cycle graph |   1,2,4,3 ,  3,4,1,2  |
  1,2,3,5,4 ,  1,4,5,2,3  | |
| 10-cycle graph |   1,3,2,5,4 ,  2,1,4,3,5  |
| 12-cycle graph |   1,2,3,5,4 ,  2,1,4,3,5  |
| Franklin graph |   1,2,3,5,4 ,  1,2,4,3,5 ,  2,1,3,5,4  |
  1,2,3,4,5,7,6 ,  1,2,3,4,6,5,7 ,  1,2,4,3,5,7,6  | |
| great rhombicuboctahedral graph |   1,2,3,4,5,7,6 ,  1,2,3,4,6,5,7 ,  1,3,2,5,4,7,6  |
| icosahedral graph |   1,3,4,2 ,  2,1,4,3 ,  2,3,1,4  |
  1,3,4,2 ,  1,4,2,3 ,  2,1,4,3 ,  2,3,1,4  | |
  1,3,4,2 ,  1,4,2,3 ,  2,1,4,3 ,  2,3,1,4 ,  3,1,2,4  | |
| 4-Möbius ladder |   1,2,4,3 ,  2,1,4,3 ,  3,4,1,2  |
| octahedral graph |   1,3,2 ,  2,1,3 ,  2,3,1  |
  1,2,4,3 ,  1,3,2,4 ,  1,3,4,2  | |
  1,2,4,3 ,  1,3,2,4 ,  1,3,4,2 ,  1,4,2,3  | |
  1,2,4,5,3 ,  2,1,4,5,3  | |
  1,2,4,5,3 ,  2,1,4,5,3  | |
| Pappus graph |   1,2,3,4,6,5 ,  2,3,1,5,4,6  |
| 2-path graph |   2,1  |
  1,3,2  | |
| pentatope graph |   2,3,4,5,1 ,  3,4,5,1,2  |
| 5-prism graph |   1,3,2,5,4 ,  2,4,1,5,3  |
  1,3,2,5,4 ,  2,4,1,5,3  | |
| 6-prism graph |   1,2,3,5,4 ,  2,1,4,5,3  |
  1,2,3,5,4 ,  2,1,4,5,3  | |
| small rhombicosidodecahedral graph |   1,2,4,5,3 ,  3,4,2,5,1  |
| small rhombicuboctahedral graph |   1,3,4,2 ,  2,3,4,1  |
  1,3,4,2 ,  1,4,2,3 ,  2,3,4,1  | |
  1,3,4,2 ,  1,4,2,3 ,  2,3,4,1 ,  4,1,2,3  | |
  1,2,4,5,3 ,  1,3,4,5,2  | |
| snub cubical graph |   1,2,4,3 ,  2,3,1,4 ,  2,3,4,1  |
  1,2,4,3 ,  2,3,1,4 ,  2,3,4,1 ,  3,1,2,4  | |
  1,2,4,3 ,  2,3,1,4 ,  2,3,4,1 ,  3,1,2,4 ,  4,1,2,3  | |
| square antiprism graph |   1,2,4,3 ,  3,4,1,2 ,  3,4,2,1  |
  1,2,4,3 ,  3,4,1,2 ,  3,4,2,1 ,  4,3,1,2  | |
| square graph |   1,2,4,3 ,  2,1,3,4  |
  1,2,3,5,4 ,  1,3,2,4,5  | |
| tesseract graph |   1,2,3,4,6,5 ,  1,2,4,3,5,6 ,  3,4,2,1,5,6  |
| tetrahedral graph |   2,1,4,3 ,  3,4,2,1  |
  1,2,4,3 ,  2,1,3,4 ,  2,1,4,3  | |
  1,3,2,5,4 ,  1,4,5,3,2  | |
| triangle graph |   2,3,1  |
  1,3,4,2 ,  1,4,2,3  | |
  1,2,4,5,3 ,  1,2,5,3,4  | |
| triangular prism graph |   1,3,2 ,  2,3,1  |
  1,2,4,3 ,  1,3,4,2  | |
  1,2,4,3 ,  1,3,4,2 ,  1,4,2,3  | |
  1,2,3,5,4 ,  1,2,4,5,3  | |
| truncated cubical graph |   1,2,4,3 ,  2,3,1,4  |
  1,2,4,3 ,  2,3,1,4 ,  3,1,2,4  | |
  1,2,3,5,4 ,  1,3,4,2,5  | |
| truncated dodecahedral graph |   1,2,4,5,3 ,  3,4,1,2,5  |
| truncated icosahedral graph |   1,3,2,5,4 ,  2,3,4,5,1  |
| truncated octahedral graph |   1,2,4,3 ,  2,3,4,1  |
  1,2,4,3 ,  1,3,2,4 ,  2,1,3,4  | |
  1,2,3,5,4 ,  1,3,4,5,2  | |
| truncated tetrahedral graph |   1,3,4,2 ,  2,1,4,3  |
  1,3,4,2 ,  1,4,2,3 ,  2,1,4,3  | |
  1,2,4,5,3 ,  1,3,2,5,4  | |
utility
graph  |   1,3,2 ,  2,1,3 ,  3,2,1  |
  1,2,4,3 ,  1,3,2,4 ,  1,4,3,2  | |
  1,2,3,5,4 ,  2,3,1,5,4  | |
  1,2,3,5,4 ,  2,3,1,5,4  |
For example, the dihedral group 
is a permutation group
with 14 elements that can be generated by two elements corresponding to a reversal and a rotation,
respectively. Therefore, any two such elements give
a connected Cayley graph that has 14 nodes
and 28 directed edges. The left figure above shows
the Cayley graph for the choice of group generators
given by (7, 1, 2, 3, 4, 5, 6) and (7, 6, 5, 4, 3, 2, 1), with reversals shown in
red and rotations in blue. Any two elements corresponding
to a rotation only will give a disconnected graph,
and there are exactly 15 pairs of such elements
since there are 
ways to pick two elements from six possible nonidentity
rotations. (Here, the number 6 appears instead of 7 since
the identity element may not be a member of the
subset giving the Cayley graph.) The right figure shows
the Cayley graph for 
generated by the elements (7, 1, 2, 3, 4, 5, 6)
and (6, 7, 1, 2, 3, 4, 5), which is disconnected
since these elements do not generate the group.
The rotations generate the cyclic group subgroup
with subgroup index 2, so the two cosets
give separate connected components.
The figure above shows the Cayley graph for the alternating group 
using the elements (2, 1, 4, 3) and (2, 3, 1, 4)
as group generators, which is a directed
form of the truncated tetrahedral graph.
If three vertices of the complete graph 
are covered with differently colored stones and any stone may be moved to the empty
vertex, then the graph
of all positions forms a Cayley graph with edges indicating
neighboring positions (left figure). This corresponds to the Cayley graph of the
symmetric group 
using the elements (2,
1, 3, 4), (3, 2, 1, 4), and (4, 2, 3, 1) as group
generators. It turns out that this graph is a directed
version of the unique cubic
symmetric graph on 24 vertices (right figure).
All connected simple undirected cubic Cayley graphs on at most 5000 vertices have been enumerated (Evans and Potočnik 2026).
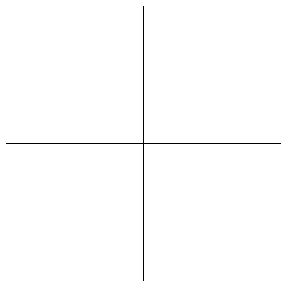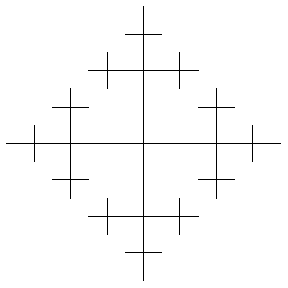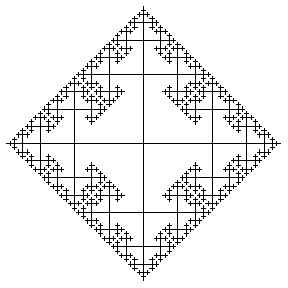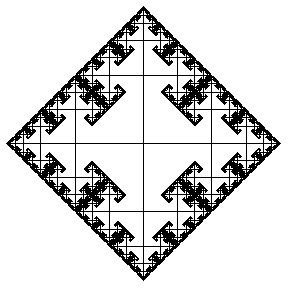
The Cayley graphs of infinite groups provide interesting geometries. For example, the Cayley graphs of the free group on two group generators are illustrated above (drawn out to successive levels), representing horizontal and vertical displacement respectively. Each new edge is drawn at half the size to give fractal images.
