A Hundred-Dollar Challenge
By Eric W. Weisstein
February 4, 2002--The January/February 2002 issue of the magazine SIAM News
contains an interesting challenge to readers. In it, Nick Trefethen
proposes 10 computational problems, each of which has a single real
number as its answer. The author has offered a $100 award to the person
or group that manages to calculate the greatest number of correct digits
by May 20, 2002. Points are awarded on the basis of one point for each
correct digit for a maximum of 10 correct points per problem.
The hundred-dollar,
hundred-digit challenge problems range in subject from numerical integration to global minimization to solution of random walks.
The complete list can be downloaded in PDF and is reproduced in
MathWorld as well as below for convenience. Solutions should
be sent to lnt@comlab.ox.ac.uk.
|
- 1. What is
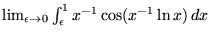 ? ?
- 2. A photon moving at speed 1 in the
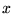 - -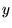 plane starts at
plane starts at 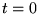 at
at
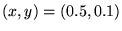 heading
due east. Around every integer lattice point
heading
due east. Around every integer lattice point 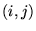 in the plane, a circular mirror of radius
in the plane, a circular mirror of radius 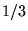 has been erected.
How far from the origin is the photon at
has been erected.
How far from the origin is the photon at 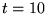 ? ?
- 3. The infinite matrix
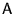 with entries
with entries 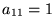 , ,
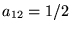 , ,
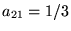 , ,
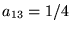 , ,
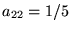 , ,
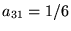 ,
etc., is a bounded operator on ,
etc., is a bounded operator on 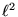 .
What is .
What is
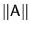 ? ?
- 4. What is the global minimum of the function
- 5. Let
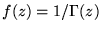 ,
where ,
where 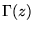 is the gamma function, and let
is the gamma function, and let 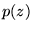 be the cubic
polynomial that best approximates
be the cubic
polynomial that best approximates 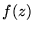 on the unit disk in the supremum norm
on the unit disk in the supremum norm
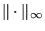 .
What
is .
What
is
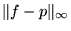 ? ?
- 6. A flea starts at
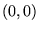 on the infinite 2D integer lattice and executes a biased random walk: At each step
it hops north or south with probability 1/4, east with probability
on the infinite 2D integer lattice and executes a biased random walk: At each step
it hops north or south with probability 1/4, east with probability
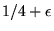 ,
and west with probability ,
and west with probability
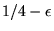 .
The probability that the flea returns to .
The probability that the flea returns to 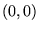 sometime during its wanderings is 1/2. What is
sometime during its wanderings is 1/2. What is
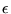 ? ?
- 7. Let
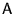 be the
be the
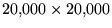 matrix whose entries are zero everywhere except for the
primes 2, 3, 5, 7, ..., 224737 along the main diagonal and the number 1 in all the positions
matrix whose entries are zero everywhere except for the
primes 2, 3, 5, 7, ..., 224737 along the main diagonal and the number 1 in all the positions 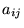 with
with
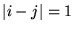 ,
2, 4, 8, ..., 16384. What is the (1, 1) entry of ,
2, 4, 8, ..., 16384. What is the (1, 1) entry of
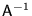 ? ?
- 8. A square plate
![$[-1, 1]\times [-1, 1]$](img34.gif) is at temperature
is at temperature 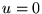 .
At time .
At time 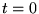 the temperature is
increased to
the temperature is
increased to 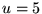 along one of the four sides while being held at
u = 0 along the other three sides,
and heat then flows into the plate according to
along one of the four sides while being held at
u = 0 along the other three sides,
and heat then flows into the plate according to
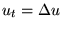 .
When
does the temperature reach .
When
does the temperature reach 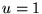 at the center of the plate?
at the center of the plate?
- 9. The integral
![$I(\alpha)=\int_0^2 [2 + \sin(10\alpha)]x^\alpha \sin(\alpha/(2- x))\,dx$](img40.gif) depends on the parameter
depends on the parameter
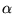 .
What is the value .
What is the value
![$\alpha\in[0, 5]$](img42.gif) at which
at which 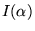 achieves its maximum?
achieves its maximum?
- 10. A particle at the center of a
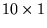 rectangle undergoes Brownian motion (i.e., 2D
random walk with infinitesimal step lengths) till it hits the boundary. What is the probability that it hits at one of
the ends rather than at one of the sides?
rectangle undergoes Brownian motion (i.e., 2D
random walk with infinitesimal step lengths) till it hits the boundary. What is the probability that it hits at one of
the ends rather than at one of the sides?
|
References