Witch of Agnesi

The "witch of Agnesi" is a curve studied by Maria Agnesi in 1748 in her book Instituzioni analitiche ad uso della gioventù italiana (the first surviving mathematical work written by a woman). The curve is also known as cubique d'Agnesi or agnésienne, and had been studied earlier by Fermat and Guido Grandi in 1703.

The name "witch" derives from a mistranslation of the term averisera ("versed sine curve," from the Latin vertere, "to turn") in the original work as avversiera ("witch" or "wife of the devil") in an 1801 translation of the work by Cambridge Lucasian Professor of Mathematics John Colson (Gray).

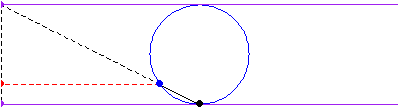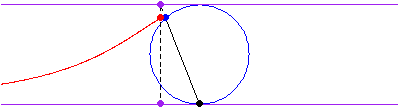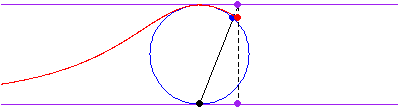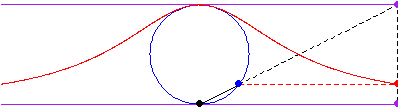
The curve is obtained by drawing a line from the origin through the circle of radius and center , then picking the point with the coordinate of the intersection with the circle and the coordinate of the intersection of the extension of line with the line .

In parametric form,

			(1)
			(2)

for , or

			(3)
			(4)

for .

The Cartesian equation can be obtained by eliminating in the parametric equations, giving

(5)

which is equivalent in functional form to the Lorentzian function.

The area between the curve and the -axis is

(6)

The curve has inflection points at . The line is an asymptote to the curve.

The curvature and tangential angle in the second parametrization are given by

			(7)
			(8)