The Weierstrass zeta function  is the quasiperiodic function defined by
is the quasiperiodic function defined by
 |
(1)
|
where  is the Weierstrass elliptic function
with invariants
is the Weierstrass elliptic function
with invariants  and
and  , with
, with
![lim_(z->0)[zeta(z;g_2,g_3)-z^(-1)]=0.](/images/equations/WeierstrassZetaFunction/NumberedEquation2.svg) |
(2)
|
As in the case of other Weierstrass elliptic functions, the elliptic invariants  and
and  are frequently suppressed for compactness. The function is implemented in the Wolfram Language as WeierstrassZeta[u,
are frequently suppressed for compactness. The function is implemented in the Wolfram Language as WeierstrassZeta[u,
 g2,
g3
g2,
g3 ].
].
Using the definition above gives
where  ,
so
,
so
![zeta(z)=z^(-1)+sum^'_(m,n=-infty)^infty[(z-Omega_(mn))^(-1)+Omega_(mn)^(-1)+zOmega_(mn)^(-2)]](/images/equations/WeierstrassZetaFunction/NumberedEquation3.svg) |
(5)
|
so  is an odd function. Integrating
is an odd function. Integrating  gives
gives
 |
(6)
|
Letting  gives
gives
 |
(7)
|
so
 |
(8)
|
Similarly,
 |
(9)
|
From Whittaker and Watson (1990),
 |
(10)
|
If  ,
then
,
then
![[zeta(x)+zeta(y)+zeta(z)]^2+zeta^'(x)+zeta^'(y)+zeta^'(z)=0](/images/equations/WeierstrassZetaFunction/NumberedEquation9.svg) |
(11)
|
(Whittaker and Watson 1990, p. 446). Also,
 |
(12)
|
(Whittaker and Watson 1990, p. 446).
The series expansion of  is given by
is given by
 |
(13)
|
where
and
 |
(16)
|
for  (Abramowitz and Stegun 1972, p. 635). The first few coefficients are therefore
(Abramowitz and Stegun 1972, p. 635). The first few coefficients are therefore
See also
Weierstrass Elliptic
Function,
Weierstrass Sigma Function
Related Wolfram sites
http://functions.wolfram.com/EllipticFunctions/WeierstrassZeta/,
http://functions.wolfram.com/EllipticFunctions/WeierstrassZetaHalfPeriodValues/
Explore with Wolfram|Alpha
References
Abramowitz, M. and Stegun, I. A. (Eds.). "Weierstrass Elliptic and Related Functions." Ch. 18 in Handbook
of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 627-671, 1972.Brezhnev, Y. V. "Uniformisation:
On the Burnside Curve  ." 9 Dec 2001. http://arxiv.org/abs/math.CA/0111150.Tölke,
F. "Spezielle Weierstraßsche Zeta-Funktionen." Ch. 8 in Praktische
Funktionenlehre, dritter Band: Jacobische elliptische Funktionen, Legendresche elliptische
Normalintegrale und spezielle Weierstraßsche Zeta- und Sigma Funktionen.
Berlin: Springer-Verlag, pp. 145-163, 1967.Whittaker, E. T.
and Watson, G. N. "Quasi-Periodic Functions. The Function
." 9 Dec 2001. http://arxiv.org/abs/math.CA/0111150.Tölke,
F. "Spezielle Weierstraßsche Zeta-Funktionen." Ch. 8 in Praktische
Funktionenlehre, dritter Band: Jacobische elliptische Funktionen, Legendresche elliptische
Normalintegrale und spezielle Weierstraßsche Zeta- und Sigma Funktionen.
Berlin: Springer-Verlag, pp. 145-163, 1967.Whittaker, E. T.
and Watson, G. N. "Quasi-Periodic Functions. The Function  " and "The Quasi-Periodicity of the Function
" and "The Quasi-Periodicity of the Function
 ."
§20.4 and 20.41 in A
Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University
Press, pp. 445-447 and 449-451, 1990.
."
§20.4 and 20.41 in A
Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University
Press, pp. 445-447 and 449-451, 1990.Referenced on Wolfram|Alpha
Weierstrass Zeta Function
Cite this as:
Weisstein, Eric W. "Weierstrass Zeta Function."
From MathWorld--A Wolfram Resource. https://mathworld.wolfram.com/WeierstrassZetaFunction.html
Subject classifications
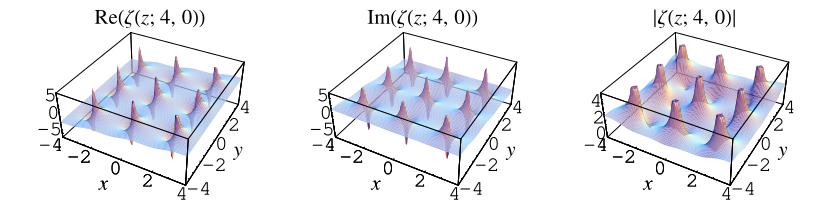
is the quasiperiodic function defined by
is the Weierstrass elliptic function
with invariants
and
, with
and
are frequently suppressed for compactness. The function is implemented in the Wolfram Language as WeierstrassZeta[u,
g2,
g3
].
![-sum^'_(m,n=-infty)^inftyint_0^z[(z-Omega_(mn))^(-2)-Omega_(mn)^(-2)]dz,](/images/equations/WeierstrassZetaFunction/Inline14.svg)
,
so
![zeta(z)=z^(-1)+sum^'_(m,n=-infty)^infty[(z-Omega_(mn))^(-1)+Omega_(mn)^(-1)+zOmega_(mn)^(-2)]](/images/equations/WeierstrassZetaFunction/NumberedEquation3.svg)
is an odd function. Integrating
gives
gives
,
then

is given by


(Abramowitz and Stegun 1972, p. 635). The first few coefficients are therefore