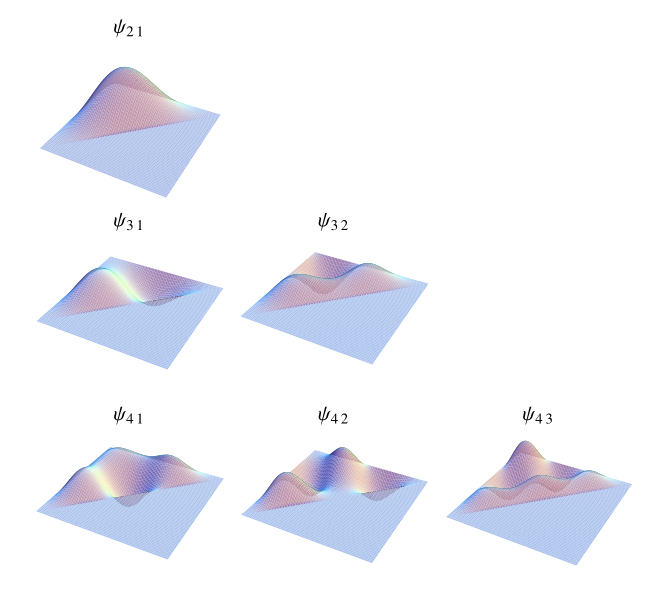
The equation of motion for a membrane shaped as a right isosceles triangle of length on a side and with the sides oriented along the positive
and
axes is given by
![psi(x,y,t)=[C_(pq)cos(omega_(pq)t)+D_(pq)sin(omega_(pq)t)][sin((ppix)/c)sin((qpiy)/c)-sin((qpix)/c)sin((ppiy)/c)],](/images/equations/WaveEquationTriangle/NumberedEquation1.svg) |
where
and ,
integers with
. This solution can be obtained by subtracting two wave
solutions for a square membrane with the indices reversed. Since points on the diagonal
which are equidistant from the center must have the same wave equation solution (by
symmetry), this procedure gives a wavefunction which will vanish along the diagonal
as long as
and
are both even
or odd. We must further restrict
the modes since those with
give wavefunctions which are just the negative
of
and
give an identically zero wavefunction.
The plots above show the lowest order spatial modes.