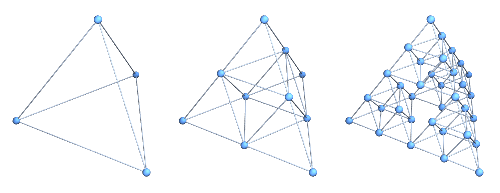
The th-order
Sierpiński tetrahedron graph is the connectivity graph of black triangles in
the
th
iteration of the tetrix fractal. The first three iterations
are shown above. It is the three-dimensional analog of the Sierpiński
gasket graph and can be further generalized to higher dimensions (D. Knuth,
pers. comm., May 1, 2022).
The -Sierpiński
tetrahedron graph has
vertices and
edges.