TOPICS
Search

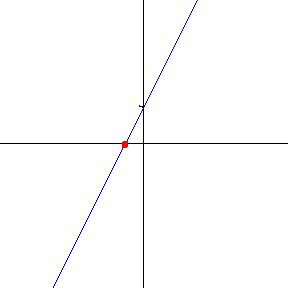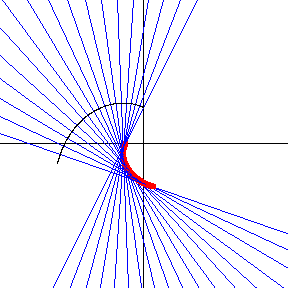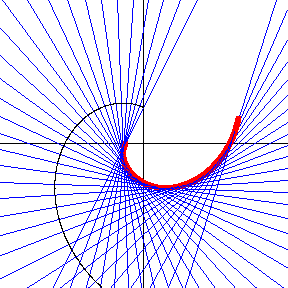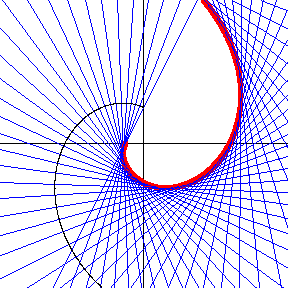
Logarithmic Spiral Evolute

DOWNLOAD Mathematica NotebookDownload Wolfram Notebook
Logarithmic spiral evolute

For a logarithmic spiral given parametrically as

x=ae^(bt)cost
(1)
y=ae^(bt)sint,
(2)

evolute is given by

x_e=-abe^(bt)sint
(3)
y_e=abe^(bt)cost.
(4)

As first shown by Johann Bernoulli, the evolute of a logarithmic spiral is therefore another logarithmic spiral, having b^'=b and a^'=ab,

In some cases, the evolute is identical to the original, as can be demonstrated by making the substitution to the new variable

t=phi-1/2pi+/-2npi.
(5)

Then the above equations become

x_e=-abe^(b(phi-pi/2+/-2npi))sin(phi-pi/2+/-2npi)
(6)
=abe^(bphi)e^(b(-pi/2+/-2npi))cosphi
(7)
y_e=abe^(b(phi-pi/2+/-2npi))cos(phi-pi/2+/-2npi)
(8)
=abe^(bphi)e^(b(-pi/2+/-2npi))sinphi,
(9)

which are equivalent to the form of the original equation if

be^(b(-1/2pi+/-2npi))=1
(10)
lnb+b(-1/2pi+/-2npi)=0
(11)
(lnb)/b=1/2pi∓2npi=-(2n-1/2)pi,
(12)

where only solutions with the minus sign in ∓ exist. Solving gives the values summarized in the following table.

nb_npsi=cot^(-1)b_n
10.2744106319...74 degrees39^'18.53^('')
20.1642700512...80 degrees40^'16.80^('')
30.1218322508...83 degrees03^'13.53^('')
40.0984064967...84 degrees22^'47.53^('')
50.0832810611...85 degrees14^'21.60^('')
60.0725974881...85 degrees50^'51.92^('')
70.0645958183...86 degrees18^'14.64^('')
80.0583494073...86 degrees39^'38.20^('')
90.0533203211...86 degrees56^'52.30^('')
100.0491732529...87 degrees11^'05.45^('')

Explore with Wolfram|Alpha

References

Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press, pp. 60-64, 1991.

Referenced on Wolfram|Alpha

Logarithmic Spiral Evolute

Cite this as:

Weisstein, Eric W. "Logarithmic Spiral Evolute." From MathWorld--A Wolfram Resource. https://mathworld.wolfram.com/LogarithmicSpiralEvolute.html

Subject classifications