Let  be the divisor function. Then
be the divisor function. Then
where  is the Euler-Mascheroni constant. Ramanujan
independently discovered a less precise version of this theorem (Berndt 1985).
is the Euler-Mascheroni constant. Ramanujan
independently discovered a less precise version of this theorem (Berndt 1985).
See also
Divisor Function,
Robin's
Theorem
Explore with Wolfram|Alpha
References
Berndt, B. C. Ramanujan's Notebooks: Part I. New York: Springer-Verlag, p. 94, 1985.Gronwall,
T. H. "Some Asymptotic Expressions in the Theory of Numbers." Trans.
Amer. Math. Soc. 14, 113-122, 1913.Nicolas, J.-L. "On
Highly Composite Numbers." In Ramanujan
Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign,
June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and
R. A. Rankin). Boston, MA: Academic Press, pp. 215-244, 1988.Robin,
G. "Grandes valeurs de la fonction somme des diviseurs et hypothese de Riemann."
J. Math. Pures Appl. 63, 187-213, 1984.Referenced on Wolfram|Alpha
Gronwall's Theorem
Cite this as:
Weisstein, Eric W. "Gronwall's Theorem."
From MathWorld--A Wolfram Resource. https://mathworld.wolfram.com/GronwallsTheorem.html
Subject classifications
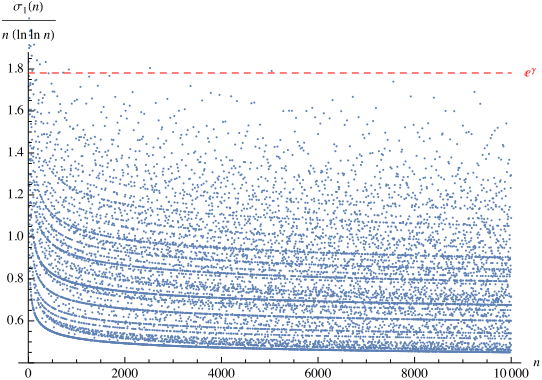
be the divisor function. Then
is the Euler-Mascheroni constant. Ramanujan
independently discovered a less precise version of this theorem (Berndt 1985).

be the divisor function. Then
is the Euler-Mascheroni constant. Ramanujan
independently discovered a less precise version of this theorem (Berndt 1985).