Double Factorial -- from Wolfram MathWorld

Double Factorial

The double factorial of a positive integer is a generalization of the usual factorial defined by

n!!={n·(n-2)...5·3·1 n>0 odd; n·(n-2)...6·4·2 n>0 even; 1 n=-1,0.

(1)

Note that , by definition (Arfken 1985, p. 547).

The origin of the notation appears not to not be widely known and is not mentioned in Cajori (1993).

For , 1, 2, ..., the first few values are 1, 1, 2, 3, 8, 15, 48, 105, 384, ... (OEIS A006882). The numbers of decimal digits in for , 1, ... are 1, 4, 80, 1285, 17831, 228289, 2782857, 32828532, ... (OEIS A114488).

The double factorial is implemented in the Wolfram Language as n!! or Factorial2[n].

The double factorial is a special case of the multifactorial.

The double factorial can be expressed in terms of the gamma function by

(2)

(Arfken 1985, p. 548).

The double factorial can also be extended to negative odd integers using the definition

			(3)
			(4)

for , 1, ... (Arfken 1985, p. 547).

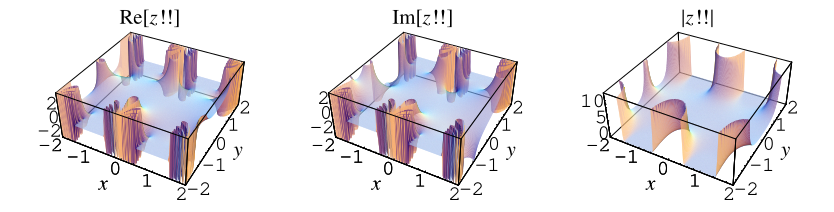
Similarly, the double factorial can be extended to complex arguments as

(5)

There are many identities relating double factorials to factorials. Since

(2n+1)!!2^nn!
=[(2n+1)(2n-1)...1][2n][2(n-1)][2(n-2)]...2·1
=[(2n+1)(2n-1)...1][2n(2n-2)(2n-4)...2]
=(2n+1)(2n)(2n-1)(2n-2)(2n-3)(2n-4)...2·1
=(2n+1)!,

(6)

it follows that . For , 1, ..., the first few values are 1, 3, 15, 105, 945, 10395, ... (OEIS A001147).

Also, since

			(7)
			(8)
			(9)

it follows that . For , 1, ..., the first few values are 1, 2, 8, 48, 384, 3840, 46080, ... (OEIS A000165).

Finally, since

(2n-1)!!2^nn!
=[(2n-1)(2n-3)...1][2n][2(n-1)][2(n-2)]...2(1)
=(2n-1)(2n-3)...1][2n(2n-2)(2n-4)...2]
=2n(2n-1)(2n-2)(2n-3)(2n-4)...2(1)
=(2n)!,

(10)

it follows that

(11)

For odd,

			(12)
			(13)
			(14)

For even,

			(15)
			(16)
			(17)

Therefore, for any ,

(18)

(19)

The double factorial satisfies the beautiful series

			(20)
			(21)
			(22)

The latter gives rhe sum of reciprocal double factorials in closed form as

			(23)
			(24)
			(25)

(OEIS A143280), where is a lower incomplete gamma function. This sum is a special case of the reciprocal multifactorial constant.

A closed-form sum due to Ramanujan is given by

(26)

(Hardy 1999, p. 106). Whipple (1926) gives a generalization of this sum (Hardy 1999, pp. 111-112).

References

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 544-545 and 547-548, 1985.

Meserve, B. E. "Double Factorials." Amer. Math. Monthly 55, 425-426, 1948.

Sloane, N. J. A. Sequences A000165/M1878, A001147/M3002, A006882/M0876, A114488, and A143280 in "The On-Line Encyclopedia of Integer Sequences."

Whipple, F. J. W. "On Well-Poised Series, Generalised Hypergeometric Series Having Parameters in Pairs, Each Pair with the Same Sum." Proc. London Math. Soc. 24, 247-263, 1926.

Double Factorial

See also

Related Wolfram sites

Explore with Wolfram|Alpha

References

Referenced on Wolfram|Alpha

Cite this as:

Subject classifications