A root of the domination polynomial is called a domination root (Akbari et al. 2010).
The set of distinct domination roots of a given graph with domination polynomial
may be denoted
(Akbari et al. 2010). Akbari et al. (2010)
showed that if a graph
has two distinct domination roots, then
. Furthermore, if
is a graph with no pendant vertex and
, then the elements of
must be 0,
, or
(Akbari et al. 2010). If pendant vertices
are allowed for three distinct domination roots, then
may also include
.
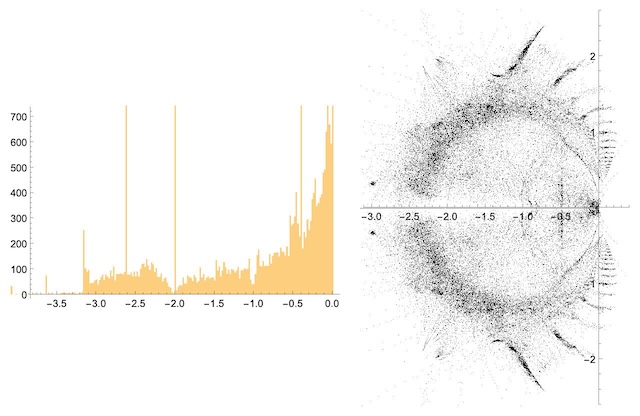
The plots above show a histogram of domatic roots along the real axis and the positions of domatic roots in the complex plane for graphs in GraphData.
The smallest real domination roots appear to occur for star graphs, corresponding to the smallest real roots of their domination
polynomials .
Akbari et al. (2010) found that no graphs on 6 or fewer vertices contain a domination root of
and conjectured that this hold for all graphs. This is true for all graphs in GraphData,
as suggested in the histogram above, as well as for all graphs up to 10 vertices
(E. Weisstein, Nov. 26, 2024). Furthermore, the only integers that occur
among the domination roots of these graphs are
and 0 (E. Weisstein, Dec. 1, 2024).