TOPICS
Search

e Continued Fraction

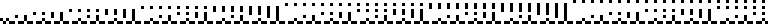
e continued fraction binary plot

The e continued fraction is the simple continued fraction of e, namely [2; 1, 2, 1, 1, 4, 1, 1, 6, ...] (OEIS A003417). This continued fraction is sometimes known as Euler's continued fraction. A plot of the first 256 terms of the continued fraction represented as a sequence of binary bits is shown above.

The convergents can be given in closed form as ratios of confluent hypergeometric functions of the first kind (Komatsu 2007ab), with the first few being 2, 3, 8/3, 11/4, 19/7, 87/32, 106/39, 193/71, ... (OEIS A007676 and A007677). For successive convergents p_n/q_n, the values of |_-log_(10)|e-p_n/q_n|_| are 0, 0, 1, 1, 2, 3, 3, 4, 5, 5, ... (OEIS A114539), where |_x_| is the floor function.

Other continued fraction representations are

(e-1)/(e+1)=[0;2,6,10,14,...]
(1)
e-1=[1;1,2,1,1,4,1,1,6,...]
(2)
1/2(e-1)=[0;1,6,10,14,...]
(3)

(Olds 1963, pp. 135-136). Not only the continued fraction of e, but also those of rational powers of e show regularity, for example

e^(1/2)=[1;1,1,1,5,1,1,9,1,1,13,...]
(4)
e^(1/3)=[1;2,1,1,8,1,1,14,1,1,20,...]
(5)
e^(1/4)=[1;3,1,1,11,1,1,19,1,1,27,...]
(6)
e^(1/5)=[1;4,1,1,14,1,1,24,1,1,34,...].
(7)

A beautiful non-simple continued fraction for e is given by

e=2+1/(1+1/(2+2/(3+3/...)))
(8)

(Wall 1948, p. 348).

EKhinchinLevy

Let the continued fraction of e be denoted [a_0;a_1,a_2,...], and let q_n be the denominator of the convergent [a_0;a_1,...,a_n]. Then plots above show successive values of a_1^(1/1), (a_1a_2)^(1/2), ..., (a_1a_2...a_n)^(1/n) (left figure) and q_n^(1/n) (right figure). Every third partial quotient grows linearly, so (a_1a_2...a_n)^(1/n) tends to infinity. The inequality q_n>=a_1a_2...a_n shows that q_n^(1/n) also tends to infinity. Thus e belongs to the exceptional set of measure 0 for which these limits differ from Khinchin's constant and the Lévy constant, respectively.

e has a very regular Engel expansion, namely 1, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ... (OEIS A028310).

See also

e, e Digits, Euler's Continued Fraction

Explore with Wolfram|Alpha

References

Cohn, H. "A Short Proof of the Simple Continued Fraction Expansion of e." Amer. Math. Monthly 113, 57-62, 2006.Komatsu, T. "Some Combinatorial Properties of the Leaping Convergents." Integers: Elec. J. Combin. Num. Th. 7, 1-10, 2007a.Komatsu, T. "Some Combinatorial Properties of the Leaping Convergents." In Proceedings of the Integers Conference 2005 in Celebration of the 70th Birthday of Ronald Graham Held at the University of West Georgia, Carrollton, GA, October 27-30, 2005 (Ed. B. Landman, M. B. Nathanson, J. Nesetril, R. J. Nowakowski, and C. Pomerance). Berlin, Germany: de Gruyter, pp. 315-325, 2007b.Olds, C. D. Continued Fractions. New York: Random House, 1963.Olds, C. D. "The Simple Continued Fraction Expression of e." Amer. Math. Monthly 77, 968-974, 1970.Sloane, N. J. A. Sequences A003417/M0088, A007676/M0869, A007677/M2343, A028310, and A114539 in "The On-Line Encyclopedia of Integer Sequences."Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.

Referenced on Wolfram|Alpha

e Continued Fraction

Cite this as:

Weisstein, Eric W. "e Continued Fraction." From MathWorld--A Wolfram Resource. https://mathworld.wolfram.com/eContinuedFraction.html

Subject classifications