Steiner Chain

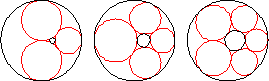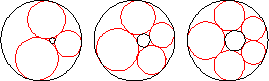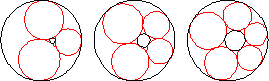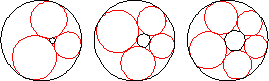
Given two circles with one interior to the other, if small tangent circles can be inscribed around the region between the two circles such that the final circle is tangent to the first, the circles form a Steiner chain.

The simplest way to construct a Steiner chain is to perform an inversion on a symmetrical arrangement on circles packed between a central circle of radius and an outer concentric circle of radius (Wells 1991). In this arrangement,

(1)

so the ratio of the radii for the small and large circles is

(2)

In addition, the radii of the circles in the ring are

(3)

and their centers are located at a distance

(4)

from the origin.

To transform the symmetrical arrangement into a Steiner chain, take an inversion center which is a distance from the center of the symmetrical figure. Then the radii and of the outer and center circles become

			(5)
			(6)

respectively. Equivalently, a Steiner chain results whenever the inversive distance between the two original circles is given by

			(7)
			(8)

(Coxeter and Greitzer 1967).

The centers of the circles in a Steiner chain lie on an ellipse (Ogilvy 1990, p. 57). The lines of tangency passing through the contact points of neighboring circles in the chain are concurrent in a point. Furthermore, this is the same point at which the lines through the contact points of the inner and outer circles also concur (Wells 1991, p. 245).

Steiner's porism states that if a Steiner chain is formed from one starting circle, then a Steiner chain is also formed from any other starting circle. A Steiner chain may also close after several loops around the central circle, in which case a Steiner chain will also be formed after the same number of loops from any starting point.