Arbelos

The term "arbelos" means shoemaker's knife in Greek, and this term is applied to the shaded area in the above figure which resembles the blade of a knife used by ancient cobblers (Gardner 1979). Archimedes himself is believed to have been the first mathematician to study the mathematical properties of this figure. The position of the central notch is arbitrary and can be located anywhere along the diameter.

The arbelos satisfies a number of unexpected identities (Gardner 1979, Schoch).

1. Call the diameters of the left and right semicircles and , respectively, so the diameter of the enclosing semicircle is 1. Then the arc length along the bottom of the arbelos is

(1)

so the arc length along the enclosing semicircle is the same as the arc length along the two smaller semicircles.

2. Draw the perpendicular from the tangent of the two semicircles to the edge of the large circle. Then the area of the arbelos is the same as the area of the circle with diameter . Let and , then simultaneously solve the equations

			(2)
			(3)
			(4)

for the sides

			(5)
			(6)
			(7)

3. The circles and inscribed on each half of on the arbelos (called Archimedes' circles) each have diameter , or radius .

The positions of the circles can be found using the triangles shown above. The lengths of the horizonal legs and hypotenuses are known as indicated, so the vertical legs can be found using the Pythagorean theorem. This then gives the centers of the circles as

			(8)
			(9)

and

			(10)
			(11)

4. Let be the point at which the circle centered at and of radius intersects the enclosing semicircle, and let be the point at which the circle centered at of radius intersects the enclosing semicircle. Then the smallest circle passing through and tangent to is equal to the smallest circle passing through and tangent to (Schoch). Moreover, the radii of these circles are the same as Archimedes' circles. Solving

(12)

(13)

gives , so the center of is

			(14)
			(15)

Similarly, solving

(16)

(17)

gives , so the center of is

			(18)
			(19)

5. The Apollonius circle of the circles with arcs , , and is located at a position

			(20)
			(21)

and has radius equal to that of Archimedes' circles (Schoch), as does the smallest circle passing through and tangent to .

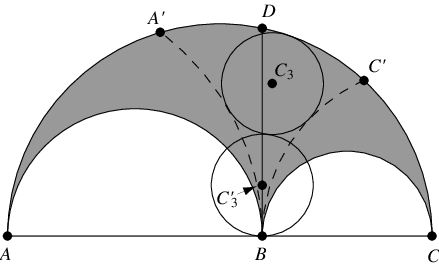
Furthermore, letting be the line parallel to through the center of circle , the circle with center on and tangent to the small semicircles of the arbelos also has radius (Schoch). The position of the center of is given by

			(22)
			(23)
			(24)

The vertical position of is

			(25)
			(26)

6. Let be the midpoint of , and let be the midpoint of . Then draw the semicircle having as a diameter with center . This circle has radius

$R_(PQ)=1/2{1-1/2[r+(1-r)]}=1/4.$

(27)

The smallest circle through touching arc then has radius (Schoch). Using similar triangles, the center of this circle is at

			(28)
			(29)

Similarly, let be the point of intersection of and the semicircle , then the circle through , , and also has radius (Schoch). The center of this circle is at

			(30)
			(31)

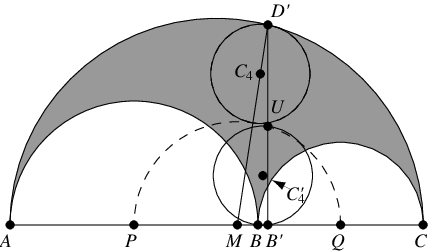
Consider the circle of radius which is tangent to the two interior semicircles. Its position and radius are obtained by solving the simultaneous equations

(32)

(33)

(34)

giving

			(35)
			(36)
			(37)

Letting be the smallest circle through and tangent to , the radius of is therefore (Schoch), and its center is located at

			(38)
			(39)

7. Within each small semicircle of an arbelos, construct arbeloses similar to the original. Then the circles and are congruent and have radius (Schoch). Moreover, connect the midpoints of the arcs and their cusp points to form the rectangles and . Then these rectangles are similar with respect to the point (Schoch). This point lies on the line , and the circle with center and radius also has radius , so has coordinates . The following tables summarized the positions of the rectangle vertices.

	coordinates		coordinates

8. Let be the perpendicular bisector of , let be the cusp of the arbelos and lie above it, let and be the tops of the large and small semicircles, respectively. Let intersect the lines and in points and , respectively. Then the smallest circle passing through and tangent to arc at , the smallest circle through and tangent to the outside semicircle at , and the circle with diameter are all Archimedean circles (Schoch). The circle is called the Bankoff circle, and is also the circumcircle of the point and tangent points and of the first Pappus circle. The centers of the circles , , and are given by

			(40)
			(41)
			(42)
			(43)
			(44)
			(45)

Rather amazingly, the points , , , , , , and are concyclic (Schoch) in a circle with center and radius

(46)

9. The smallest circumcircle of Archimedes' circles has an area equal to that of the arbelos.

10. The line tangent to the semicircles and contains the point and which lie on the lines and , respectively. Furthermore, and bisect each other, and the points , , , and are concyclic.

11. Construct a chain of tangent circles starting with the circle tangent to the two small ones and large one. This chain is called a Pappus chain, and the centers of its circles lie on an ellipse having foci at the centers of the semicircles bounding it. Furthermore, the diameter of the th circle is ()th the perpendicular distance to the base of the semicircle. This result is most easily proven using inversion, but was known to Pappus, who referred to it as an ancient theorem (Hood 1961, Cadwell 1966, Gardner 1979, Bankoff 1981).

12. The common tangent (see 10) and the common tangent of the great semicircle and the first Pappus circle meet on line .

13. If divides in the golden ratio , then the circles in the chain satisfy a number of other special properties (Bankoff 1955).

Arbelos

Wolfram Web Resources