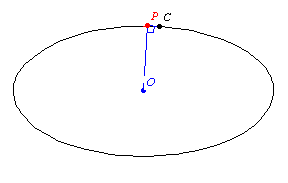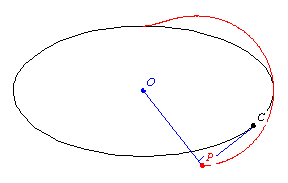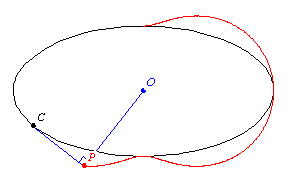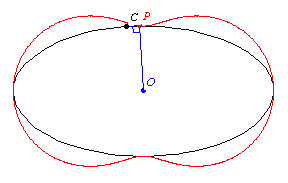
The pedal of a curve with respect to a point is the locus of the foot of the perpendicular from to the tangent to the curve. More precisely, given a curve , the pedal curve of with respect to a fixed point (called the pedal point) is the locus of the point of intersection of the perpendicular from to a tangent to . The parametric equations for a curve relative to the pedal point are given by

			(1)
			(2)

If a curve is the pedal curve of a curve , then is the negative pedal curve of (Lawrence 1972, pp. 47-48).

When a closed curve rolls on a straight line, the area between the line and roulette after a complete revolution by any point on the curve is twice the area of the pedal curve (taken with respect to the generating point) of the rolling curve.

Ameseder, A. "Ueber Fusspunktcurven der Kegelschnitte." Archiv Math. u. Phys. 64, 143-144, 1879.

Ameseder, A. "Zur Theorie der Fusspunktencurven der Kegelschnitte." Archiv Math. u. Phys. 64, 145-163, 1879.

Gray, A. "Pedal Curves." §5.8 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 117-125, 1997.

Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, p. 25, 1999.

Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 46-49 and 204, 1972.

Lockwood, E. H. "Pedal Curves." Ch. 18 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 152-155, 1967.

Porteous, I. R. Geometric Differentiation for the Intelligence of Curves and Surfaces. Cambridge, England: Cambridge University Press, 1994.

Trott, M. The Mathematica GuideBook for Graphics. New York: Springer-Verlag, p. 19, 2004. http://www.mathematicaguidebooks.org/.

Ueda, K. In Mathematical Methods for Curves and Surfaces (Ed. T. Lyche and L. L. Shumaker). Nashville, TN: Vanderbilt University Press, 2001.

Yates, R. C. "Pedal Curves." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 160-165, 1952.

Zwikker, C. The Advanced Geometry of Plane Curves and Their Applications. New York: Dover, pp. 150-158, 1963.

CITE THIS AS:

Weisstein, Eric W. "Pedal Curve." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PedalCurve.html