The three circumcircles through the triangle centroid of a given triangle
and the pairs of the vertices of the second
Brocard triangle are called the McCay circles (Johnson 1929, p. 306).
The circumcircle of their centers (i.e., of the second Brocard triangle) is therefore the Brocard circle.
The -McCay circle has center function
and radius,
1/3 that of the Neuberg circle, where is the Brocard angle
(Johnson 1929, p. 307).
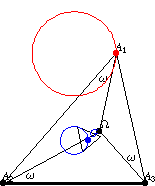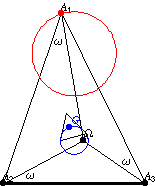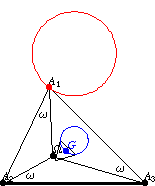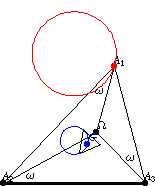
If the polygon vertex of a triangle describes a Neuberg circle
, then its triangle centroid
describes one of the McCay circles (Johnson
1929, p. 290). In the above figure, the inner triangle is the second Brocard
triangle of
,
whose two indicated edges are concyclic with
on the McCay circle.