Icosidodecahedron

In general, an icosidodecahedron is a 32-faced polyhedron. A number of such solids are illustrated above.

Make Your Own Icosidodecahedron

Print & fold

Print in 3D

"The" (quasiregular) icosidodecahedron is the 32-faced Archimedean solid with faces . It is one of the two convex quasiregular polyhedra. It is illustrated above together with a wireframe version and a net that can be used for its construction.

It is also the uniform polyhedron with Maeder index 24 (Maeder 1997), Wenninger index 12 (Wenninger 1989), Coxeter index 28 (Coxeter et al. 1954), and Har'El index 29 (Har'El 1993). It has Schläfli symbol and Wythoff symbol .

Several symmetric projections of the icosidodecahedron are illustrated above.

It is implemented in the Wolfram Language as PolyhedronData["Icosidodecahedron"] or UniformPolyhedron["Icosidodecahedron"].

The polyhedron vertices of an icosidodecahedron of polyhedron edge length are , , , , , . The 30 polyhedron vertices of an octahedron 5-compound form an icosidodecahedron (Ball and Coxeter 1987). Faceted versions include the small icosihemidodecahedron and small dodecahemidodecahedron.

The regular icosidodecahedron is the convex hull of the cube-octahedron 5-compound, dodecadodecahedron, great dodecahemicosahedron, great dodecahemidodecahedron, great icosidodecahedron, great icosihemidodecahedron, third icosahedron stellation hull, octahedron 5-compound, small dodecahemicosahedron, small dodecahemidodecahedron, and small icosihemidodecahedron.

The icosidodecahedron constructed in origami is illustrated above (Kasahara and Takahama 1987, pp. 48-49). This construction uses 120 sonobè units, each made from a single sheet of origami paper.

The faces of the icosidodecahedron consist of 20 triangles and 12 pentagons. Furthermore, its 60 edges are bisected perpendicularly by those of the reciprocal rhombic triacontahedron (Ball and Coxeter 1987).

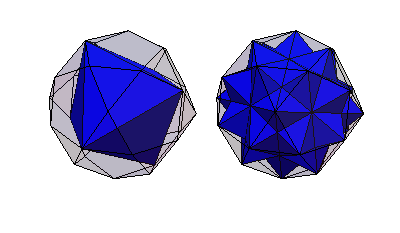
Five octahedra of edge length can be inscribed on the vertices of an icosidodecahedron of unit edge length, resulting in the beautiful octahedron 5-compound.

The dual polyhedron of the icosidodecahedron is the rhombic triacontahedron, both of which are illustrated above together with their common midsphere.

The inradius of the dual, midradius of the solid and dual, and circumradius of the solid for are

			(1)
			(2)
			(3)
			(4)
			(5)
			(6)

where is the golden ratio.

The surface area and volume for an icosidodecahedron are given by

			(7)
			(8)

The distance to the centers of the triangular and pentagonal faces are

			(9)
			(10)

The dihedral angle between triangular and pentagonal faces is

			(11)
			(12)

The unit regular icosiedodecahedron has Dehn invariant

			(13)
			(14)
			(15)

(OEIS A377606), where the first expression uses the basis of Conway et al. (1999). It can be dissected into the pentagonal orthobirotunda (E. Weisstein, Aug. 17, 2023).