Half a circle. The area of a semicircle of radius
is given by
|
(1)
| |||
|
(2)
| |||
|
(3)
|
The weighted mean of
is
|
(4)
| |||
|
(5)
|
The semicircle is the cross section of a hemisphere for any plane through the z-axis.
The perimeter of the curved boundary is given by
|
(6)
|
With , this gives
|
(7)
|
This property is sometimes, especially in the older literature, referred to as the semicircumference.
The perimeter of the semicircular lamina is then the sum of its semicircumference and diameter:
|
(8)
| |||
|
(9)
| |||
|
(10)
|
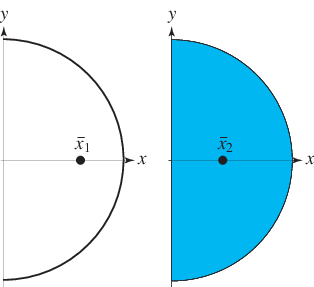
The weighted value of
of the semicircular curve is given by
|
(11)
| |||
|
(12)
| |||
|
(13)
|
so the geometric centroid is
|
(14)
|
The geometric centroid of the semicircular lamina is given by
|
(15)
|
(Kern and Bland 1948, p. 113).