MathWorld Headline News

The Gray Graph Is the Smallest Graph of Its Kind

By Eric W. Weisstein

April 9, 2002--In a paper submitted to Discrete Mathematics, a team of mathematicians has settled the question of determining the smallest cubic graph that is semisymmetric (i.e., edge- but not vertex-transitive). A cubic graph is simply a collection of vertices and edges (i.e., a graph in the graph theoretical sense) such that three edges exit each vertex, where loops connecting a vertex to itself and multiple edges between two nodes are not allowed (i.e., the graph is a so-called simple graph). An edge-transitive graph is a graph such that any two edges are equivalent under some element of its so-called automorphism group, with a vertex-transitive graph defined analogously. An automorphism group of a graph is the group (in the group theoretical sense) of functions from the graph to itself that preserve the structure of the graph.

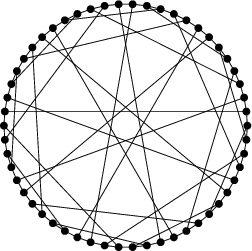
A semisymmetric cubic graph on 54 vertices was discovered by Marion C. Gray in 1932 and was first published by Bouwer (1968). This graph, illustrated above, was named the Gray graph in honor of its original discoverer. Since its publication, the Gray graph has remained the smallest known example of a cubic semisymmetric transitive. In a forthcoming paper, Malnic et al. finally demonstrate that the Gray graph is in fact the smallest such graph possible.