A transversal intersection of two submanifolds 
and 
in an ambient manifold 
is one for which, for all 
,
 |
where the vector addition is in 
, and 
denotes the tangent space
of 
at 
.
If two submanifolds do not intersect,
then they are automatically transversal. For example, two curves
in 
are transversal only if they do not intersect at
all. When 
and 
meet transversally, 
is a smooth submanifold
of the expected dimension 
.
In some sense, two submanifolds "ought" to intersect transversally and, by Sard's theorem, any intersection can be perturbed to be transversal. Intersection in homology only makes sense because an intersection can be made to be transversal.
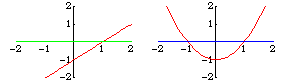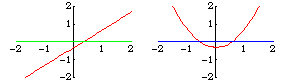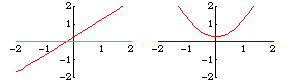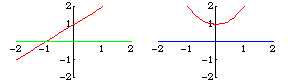
Transversality is a sufficient condition for an intersection to be stable after a perturbation. For example, the lines 
and 
intersect transversally, as do the perturbed lines 
,
and they intersect at only one point.
However, 
does not intersect 
transversally. It intersects
in one point, while 
intersects in either
zero or two points, depending on whether 
is positive or negative.
When 
,
then each point of a transversal intersection is an isolated point. If the three spaces
have a vector space orientation, then
the transversal condition means it is possible to assign a sign to the intersection.
If 
are an oriented vector basis for 
and 
are an oriented vector
basis for 
,
then the intersection is 
if 
is oriented in 
and 
otherwise.
More generally, two smooth maps 
and 
are transversal if whenever 
then 
.
