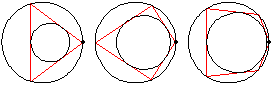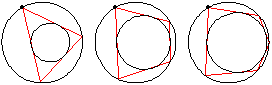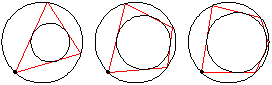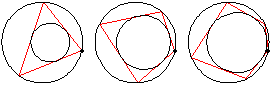
Poncelet's Porism

If an -sided Poncelet transverse constructed for two given conic sections is closed for one point of origin, it is closed for any position of the point of origin. Specifically, given one ellipse inside another, if there exists one circuminscribed (simultaneously inscribed in the outer and circumscribed on the inner) -gon, then any point on the boundary of the outer ellipse is the vertex of some circuminscribed -gon. If the conic is taken as a circle (Casey 1888, pp. 124-126) , then a polygon which has both an incenter and a circumcenter (and for which the transversals would therefore close) is called a bicentric polygon.

Amazingly, this problem is isomorphic to Gelfand's question (King 1994).

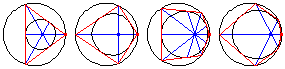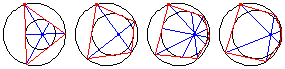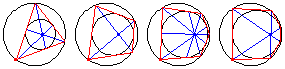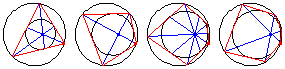
For an even-sided polygon, the diagonals are concurrent at the limiting point of the two circles, whereas for an odd-sided polygon, the lines connecting the vertices to the opposite points of tangency are concurrent at the limiting point.

Inverting about either of the two limit points gives two concentric circles. However, the -gonal sides become arcs of circles in the process, so this sort of simple inversion does not provide an automatic proof of the theorem (as happens in Steiner's porism, for example).

Fuss (1792) derived formulas not only for the bicentric quadrilateral, but also the bicentric pentagon, hexagon, heptagon, and octagon, as did Steiner (Fuss 1792; Jacobi 1823; Steiner 1827; Dörrie 1965, p. 192). Chaundy (1923) exhibited porisms for , 4, 5, 6, 7, 8, 9, 10, 12, 14, 16, 18, 20, as well as erroneous expressions for several other values (Kerawala 1947). Richelot derived the expression for . In fact, there is a general analytic expression relating the circumradius , inradius , and offset between the circumcenter and incenter for a bicentric polygon. Given , , and , define

			(1)
			(2)
			(3)

Note that since , , and are positive quantities with , .

Now let

			(4)
			(5)

and define the elliptic modulus via

(6)

Then the condition for an -gon to be bicentric is

(7)

where is a Jacobi elliptic function and is a complete elliptic integral of the first kind (Richelot 1830, Kerawala 1947). Kerawala (1947) was able to establish many porisms in simple explicit form without resorting to the use of elliptic functions.

For the two circles illustrated above, the tangent on the inner circle can be determined by solving

(8)

where

			(9)
			(10)
			(11)

is the radius of the inner circle, is the offset of the inner circle, is the given position on the outer circle, and is the angle around the inner circle at which the tangent occurs. Taking the dot product and simplifying gives

(12)

When this is solved for , the point at which the extension of this line intersects the outer circle again can be found using the standard equation of a circle-line intersection.

The degrees of the algebraic equations relating , , and for , 4, ..., are 1, 2, 3, 4, 6, 8, 9, 12, 15, 16, 21, 24, 24, 32, 36, ... (OEIS A002348; Kerawala 1947). Let the prime factorization of be written as

(13)

then in general is given by

(14)

In the following expressions, write

			(15)
			(16)
			(17)
			(18)
			(19)
			(20)
			(21)
			(22)
			(23)
			(24)
			(25)
			(26)
			(27)
			(28)
			(29)
			(30)

following Kerawala (1947), and

			(31)
			(32)

following Richelot (1830).

The equation for a bicentric triangle (), i.e., any triangle, may be variously written as

(33)

(34)

(35)

(36)

(Richelot 1830), or

(37)

(Steiner 1827; F. Gabriel-Marie 1912, pp. 497-501; Kerawala 1947; Altshiller-Court 1952, pp. 85-87; Wells 1992). The latter is sometimes known as the Euler triangle formula.

For a bicentric quadrilateral (), the radii and offset are connected by the equation

(38)

(Kerawala 1947), which expands to

(39)

(Davis; Durége; Casey 1888, pp. 109-110; F. Gabriel-Marie 1912, pp. 321 and 814-816; Johnson 1929; Dörie 1965). This can also be written

(40)

(41)

(Steiner 1827), or

(42)

(Richelot 1830).

The relationship for a bicentric pentagon () is

(43)

(Steiner 1827) or

(44)

(Richelot 1830). A number of alternative forms are given by

(45)

(46)

(47)

|e_0 e_3 e_2; e_3 e_0 e_1; e_2 e_1 e_0|=0

(48)

(49)

and

(50)

(Kerawala 1947).

For ,

(51)

(Steiner 1827),

(52)

(Richelot 1830),

(53)

(54)

(Kerawala 1947).

For ,

(55)

(Jacobi 1823, Kerawala 1947)

For ,

(56)

(Kerawala 1947), which can also be written in the form

(57)

(Richelot 1830, Jacobi 1823). The equation given by Steiner (1827) contains (at least one) typographical error.

For ,

(58)

for ,

$16p^2q^2(p^2-1)(q^2-1)[p^4q^4-(p^2-q^2)^2]^2 ={[p^4-(p^2q^2-q^2)^2]^2+[q^4-(p^2q^2-p^2)^2]^2+[p^4q^4-(p^2-q^2)^2]^2}^2$

(59)

(Richelot).

For ,

$64p^4q^4(p^2-1)(q^2-1)[p^4q^4-(p^2-q^2)^2]^2 ={[p^4-(p^2q^2-q^2)^2]^2+[q^4-(p^2q^2-p^2)^2]^2+[p^4q^4-(p^2-q^2)^2]^2}^2$

(60)

(Richelot).

For ,

(61)

For ,

(62)

(Kerawala 1947) or

$64p^4q^4(p^2-1)(q^2-1){[p^4q^4-(p^2-q^2)^2](p^2+q^2-p^2q^2)}^4 ={[p^4-(p^2q^2-q^2)^2]^2+[q^4-(p^2q^2-p^2)^2]^2+[p^4q^4-(p^2-q^2)^2]^2}^4$

(63)

(Richelot 1830).

Weill (1878) gave an algorithm for finding approximate solutions for porisms with even . The following table gives the approximate relations for fixed .

			error
6
8
10

Explore with Wolfram|Alpha

More things to try:

References

Allanson, B. "Bicentric Polygons" java applet. http://members.ozemail.com.au/~llan/bimovie.html.Altshiller-Court, N. College Geometry: A Second Course in Plane Geometry for Colleges and Normal Schools, 2nd ed., rev. enl. New York: Barnes and Noble, 1952.Appell, P. and Lacour, E. Principes de la théorie des fonctions elliptiques et applications. Paris: Gauthier-Villars, pp. 138-139 and 227-243, 1922.Baker, H. F. An Introduction to Plane Geometry. London: Cambridge University Press, 1963.Barth, W. and Bauer, T. "Poncelet Theorems." Expos. Math. 14, 125-144, 1996.Barth, W. and Michel, J. "Modular Curves and Poncelet Polygons." Math. Ann. 295, 25-49, 1993.Berger, M. Geometry I. New York: Springer-Verlag, 1994.Bos, H. J. M. "The Closure Theorem of Poncelet." Rendiconti del seminario matematico e fisico di Milano 54, 145-158, 1984.Bos, H. J. M. "Poncelet's Proof of the Closure Theorem." Sugaku seminar 25, 81-87, 1986.Bos, H. J. M.; Kers, C.; Oort, F.; and Raven, D. W. "Poncelet's Closure Theorem, Its History, Its Modern Formulation, a Comparison of Its Modern Proof with Those by Poncelet and Jacobi, and Some Mathematical Remarks Inspired by These Early Proofs." Expos. Math. 5, 289-364, 1987.Casey, J. A Sequel to the First Six Books of the Elements of Euclid, Containing an Easy Introduction to Modern Geometry with Numerous Examples, 5th ed., rev. enl. Dublin: Hodges, Figgis, & Co., 1888.Cayley, A. Philos. Mag. 5, 281-284, 1853a.Cayley, A. Philos. Mag. 6, 99-102, 1853b.Cayley, A. "Developments on the Porism of the In-and-Circumscribed Polygon." Philos. Mag. 7, 339-345, 1854.Cayley, A. Phil. Trans. Roy. Soc. London 151, 225-239, 1861.Chaundy, T. W. Proc. London Math. Soc. 22, 104-123, 1923.Chaundy, T. W. Proc. London Math. Soc. 25, 17-44, 1926.Clifford, W. K. Proc. London Math. Soc. 7, 29-38.Clifford, W. K. Proc. London Math. Soc. 7, 225-233.Clifford, W. K. Proc. Cambridge Phil. Soc., 120-123, 1868.Darboux, G. Comte Rendus de l'Acadamie de Sciences 90, 1880.Darboux, G. Principles de géométrie analytique, Vol. 3. Paris, pp. 250-287, 1917.Davis, M. A. Educ. Times 32.Dörrie, H. 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 192-193, 1965.Durége. Theorie der Elliptischen Functionen. p. 185.Emelyanov L. and Emelyanova, T. "Euler's Formula and Poncelet's Porism." Forum Geom. 1, 137-140, 2001. http://forumgeom.fau.edu/FG2001volume1/FG200120.pdf.Fuss, N. Nova Acta Petropol. 10, 1792.Fuss, N. "De Polygonis symmetrice irregularibus circulo simul inscriptis et circumscriptis." Nova Acta Petropol. 13, 166-189, 1798.F. Gabriel-Marie. Exercices de Géométrie. Tours, France: Maison Mame, 1912.Griffiths, P. and Harris, J. "A Poncelet Theorem in Space." Comment. Math. Helv. 52, 145-160, 1977.Griffiths, P. and Harris, J. "On Cayley's Explicit Solution to Poncelet's Porism." Enseign. Math. 24, 31-40, 1978.Hart. Quart. J. Math., 1857.Jacobi, C. G. J. "Ueber die Anwendung der elliptischen Transcendenten auf ein bekanntes Problem der Elementargeometrie." J. reine angew. Math. 3, 376-387, 1823. Reprinted in Gesammelte Werke, Vol. 1. Providence, RI: Amer. Math. Soc., pp. 278-293, 1969.Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 91-96, 1929.Kerawala, S. M. "Poncelet Porism in Two Circles." Bull. Calcutta Math. Soc. 39, 85-105, 1947.King, J. L. "Three Problems in Search of a Measure." Amer. Math. Monthly 101, 609-628, 1994.Lebesgue, H. "Polygones de Poncelet." Ch. 4 in Les Coniques. Paris: Gauthier-Villars, pp. 115-149, 1955. Reprint of "Exposé gémoétrique d'un mémoire de Cayley sur les Polygones de Poncelet." Ann. de la Faculté des Sci. de l'Université de Toulouse 14, 1922.Lelieuvre, A. "Sur les polygones de Poncelet." L'enseign. math. 2, 410-423, 1900.Lelieuvre, A. "Sur les polygones de Poncelet." L'enseign. math. 3, 115-117, 1901.Moutard, M. "Recherches analytiques sur les polygones simultanément inscrits et circonscrits à deux coniques." Appendix to Poncelet, J. V. Traité des propriétés projectives des figures: ouvrage utile à qui s'occupent des applications de la géométrie descriptive et d'opérations géométriques sur le terrain, Vol. 1, 2nd ed. Paris: Gauthier-Villars, pp. 535-560, 1865-66.Poncelet, J. V. Traité des propriétés projectives des figures: ouvrage utile à qui s'occupent des applications de la géométrie descriptive et d'opérations géométriques sur le terrain, Vols. 1-2, 2nd ed. Paris: Gauthier-Villars, 1865-66.Previato, E. "Poncelet's Theorem in Space." Proc. Amer. Math. Soc. 127, 2547-2556, 1999.Radić, M. "Some Relations Concerning Triangles and Bicentric Quadrilaterals in Connection with Poncelet's Closure Theorem." Math. Maced. 1, 35-58, 2003.Radić, M. "Extreme Areas of Triangles in Poncelet's Closure Theorem." Forum Geom. 4, 23-26, 2004. http://forumgeom.fau.edu/FG2004volume4/FG200403index.html.Richelot, F. J. "Anwendung der elliptischen Transcendenten auf die sphärischen Polygone; welche zugleich einem kleinen Kreise der Kugel eingescrieben und einem andern umgeschrieben sind." J. reine angew. Math. 5, 250-267, 1830.Richelot, F. J. "Über die Anwendung Einiger Formeln aus der Theorie der Elliptischen Functionen auf ein Bekanntes Problem der Geometrie." J. reine angew. Math. 38, 353-372, 1849.Rosanes, J. and Pasch, M. "Über das einem Kegelschnitte umbeschriebene und einem andern einbeschriebene Polygon." J. reine angew. Math. 64, 126-166, 1865.Rosanes, J. and Pasch, M. "Über eine algebraische Aufgabe, welche einer Gattung geometrischer Probleme zu Grunde liegt." J. reine angew. Math. 70, 169-173, 1869.Schoenberg, I. J. "On Jacobi-Bertrand Proof of a Theorem of Poncelet." In Studies in Pure Mathematics to the Memory of Paul Turán (Ed. P. Erdős). Basel, Switzerland: Birkhäuser, pp. 623-627, 1983.Sloane, N. J. A. Sequence A002348/M0549 in "The On-Line Encyclopedia of Integer Sequences."Steiner, J. §26.57 in "Aufgaben und Lehrsätze, erstere aufzulösen, leztere zu beweisen." J. reine angew. Math. 2, 289, 1827.Titchmarsh, E. C. Messenger Math. 52, 42, 1922.Weill, M. and Bützberger. "Sur les polygones inscrits et circonscrits à la fois à deux cercle." Journal de Liouville, 3me série 4, 7-32, 1878.Weill, M. "Sur une classe de polygones de Poncelet." Bull. de la Soc. Math. France 29, 199-208, 1901.Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. New York: Viking Penguin, pp. 192-193, 1992.

Referenced on Wolfram|Alpha

Poncelet's Porism

Cite this as:

Weisstein, Eric W. "Poncelet's Porism." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/PonceletsPorism.html

Poncelet's Porism

See also

Explore with Wolfram|Alpha

References

Referenced on Wolfram|Alpha

Cite this as:

Subject classifications