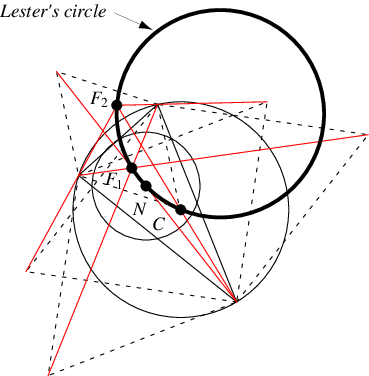
The Lester circle is the circle on which the circumcenter 
, nine-point
center 
,
and the first and second Fermat points 
and 
lie (Kimberling 1998, pp. 229-230). Besides these (Kimberling
centers 
,
, 
, and 
, respective), no other notable triangle centers lie on
the circle.
The Lester circle has circle function
![l=-(f(a,b,c)R^2[1+2cos(2A)])/(6a^2bc(a^2-b^2)(a^2-c^2)),](/images/equations/LesterCircle/NumberedEquation1.svg) |
(1)
|
where
 |
(2)
|
does not appear to have a simple form and 
does not appear in Kimberling's list of triangle centers.
The center of the Lester circle is
![alpha=bc(b^2-c^2)[2(a^2-b^2)(c^2-a^2)+3R^2(2a^2-b^2-c^2)-a^2(a^2+b^2+c^2)+a^4+b^4+c^4],](/images/equations/LesterCircle/NumberedEquation3.svg) |
(3)
|
where 
is the circumradius of the reference triangle, which
is Kimberling center 
. The radius of the Lester circle is given by
 |
(4)
|
where 
is a symmetric 16th-order polynomial that does not appear to have a simple form.
It is orthogonal to the orthocentroidal circle.
Trott, M. "A Proof of Lester's Circle Theorem."