A hyperbola (plural "hyperbolas"; Gray 1997, p. 45) is a conic section defined as the locus of all points in the plane the difference of whose
distances
and
from two fixed points (the foci
and
) separated by a distance
is a given positive constant
,
|
(1)
|
(Hilbert and Cohn-Vossen 1999, p. 3). Letting fall on the left
-intercept requires that
|
(2)
|
so the constant is given by ,
i.e., the distance between the
-intercepts (left figure above). The hyperbola has the important
property that a ray originating at a focus
reflects in such a way that the outgoing path lies along
the line from the other focus through the point of intersection
(right figure above).
The special case of the rectangular hyperbola, corresponding to a hyperbola with eccentricity , was first studied by Menaechmus. Euclid and Aristaeus
wrote about the general hyperbola, but only studied one branch of it. The hyperbola
was given its present name by Apollonius, who was the first to study both branches.
The focus and conic
section directrix were considered by Pappus (MacTutor Archive). The hyperbola
is the shape of an orbit of a body on an escape trajectory (i.e., a body with positive
energy), such as some comets, about a fixed mass, such as the sun.
|
|
|
The hyperbola can be constructed by connecting the free end of a rigid bar
, where
is a focus, and the other focus
with a string
. As the bar
is rotated about
and
is kept taut against the bar (i.e., lies on the bar), the
locus of
is one branch of a hyperbola (left figure above; Wells 1991).
A theorem of Apollonius states that for a line segment tangent to the hyperbola at
a point
and intersecting the asymptotes at points
and
,
then
is constant, and
(right figure above; Wells 1991).
Let the point
on the hyperbola have Cartesian coordinates
, then the definition of the hyperbola
gives
|
(3)
|
Rearranging and completing the square gives
|
(4)
|
and dividing both sides by
results in
|
(5)
|
By analogy with the definition of the ellipse, define
|
(6)
|
so the equation for a hyperbola with semimajor axis parallel to the x-axis
and semiminor axis
parallel to the y-axis is
given by
|
(7)
|
or, for a center at the point instead of
,
|
(8)
|
Unlike the ellipse, no points of the hyperbola actually lie on the semiminor axis, but rather the ratio
determines the vertical scaling of
the hyperbola. The eccentricity
of the hyperbola (which always satisfies
) is then defined as
 |
(9)
|
In the standard equation of the hyperbola, the center is located at , the foci are at
, and the vertices are at
. The so-called asymptotes
(shown as the dashed lines in the above figures) can be found by substituting 0 for
the 1 on the right side of the general equation (8),
|
(10)
|
and therefore have slopes .
The special case
(the left diagram above) is known as a rectangular
hyperbola because the asymptotes are perpendicular.
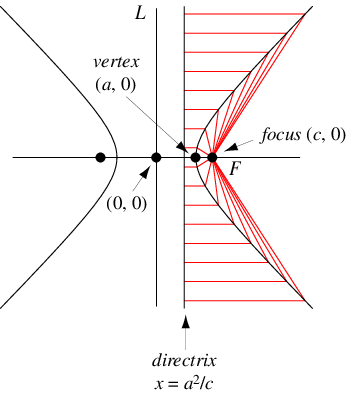
The hyperbola can also be defined as the locus of points whose distance from the focus is proportional to the horizontal distance from a vertical
line
known as the conic
section directrix, where the ratio is
. Letting
be the ratio and
the distance from the center at which the directrix lies,
then
|
(11)
| |||
|
(12)
|
where is therefore simply the eccentricity
.
Like noncircular ellipses, hyperbolas have two distinct foci and two associated conic section directrices, each conic section directrix being perpendicular to the line joining the two foci (Eves 1965, p. 275).
The focal parameter of the hyperbola is
 |
(13)
| ||
|
(14)
| |||
|
(15)
|
In polar coordinates, the equation of a hyperbola centered at the origin (i.e., with ) is
|
(16)
|
In polar coordinates centered at a focus,
|
(17)
|
as illustrated above.
The two-center bipolar coordinates equation with origin at a focus is
|
(18)
|
Parametric equations for the right branch of a hyperbola are given by
|
(19)
| |||
|
(20)
|
where is the hyperbolic
cosine and
is the hyperbolic sine, which ranges over the
right branch of the hyperbola.
A parametric representation which ranges over both branches of the hyperbola is
|
(21)
| |||
|
(22)
|
with and discontinuities at
. The arc
length, curvature, and tangential
angle for the above parametrization are
 |
(23)
| ||
 |
(24)
| ||
|
(25)
|
where is an elliptic
integral of the second kind.
The special affine curvature of the hyperbola is
|
(26)
|
The locus of the apex of a variable cone containing an ellipse fixed in three-space is a hyperbola through the foci of the ellipse. In addition, the locus of the apex of a cone containing that hyperbola is the original ellipse. Furthermore, the eccentricities of the ellipse and hyperbola are reciprocals.