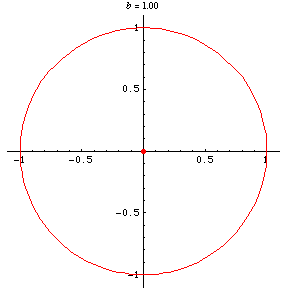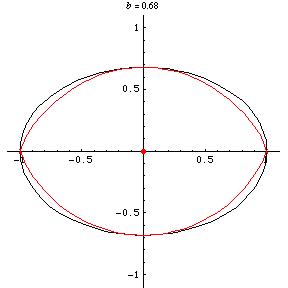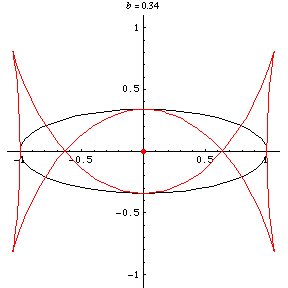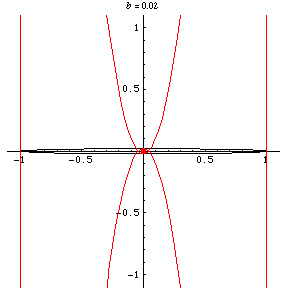
For an ellipse with parametric equations
|
(1)
| |||
|
(2)
|
the negative pedal curve with respect to the origin has parametric equations
|
(3)
| |||
|
(4)
| |||
|
(5)
| |||
|
(6)
| |||
|
(7)
| |||
 |
(8)
|
where
|
(9)
|
is the distance between the ellipse center and one of its foci and
 |
(10)
|
is the eccentricity. For , the base curve is a circle, whose negative pedal curve
with respect to the origin is also a circle. For
, the curve becomes a "squashed"
ellipse. For
, the curve has four cusps
and two ordinary double points and is known
as Talbot's curve (Lockwood 1967, p. 157).
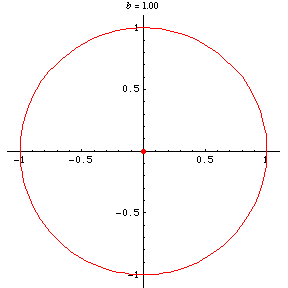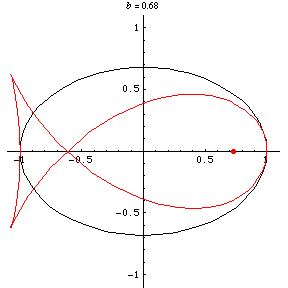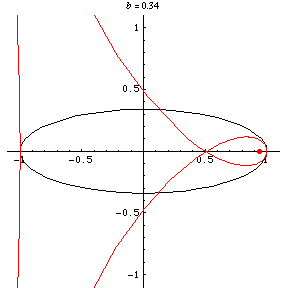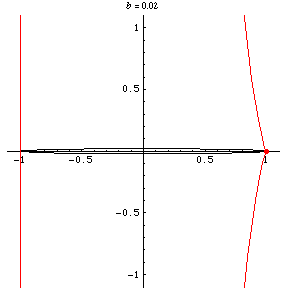
Taking the pedal point at a focus (i.e., )
gives the negative pedal curve
|
(11)
| |||
|
(12)
|
Lockwood (1957) terms this family of curves Burleigh's ovals. As a function of the aspect ratio of an ellipse, the neagtive pedal curve varies in shape
from a circle (at
) to an ovoid (for
) to a fish-shaped curve with a node and
two cusps to a line plus a loop to a line plus a cusp.
The special case of the negative pedal curve for pedal point and
(i.e.,
) is here dubbed the fish
curve.