The deltoidal hexecontahedron is the 60-faced dual polyhedron of the small rhombicosidodecahedron. It is sometimes also called the trapezoidal hexecontahedron (Holden 1971, p. 55), strombic hexecontahedron, or dyakis hexecontahedron (Unkelbach 1940). It is illustrated above together with a wireframe version and a net that can be used for its construction.
It is Wenninger dual .
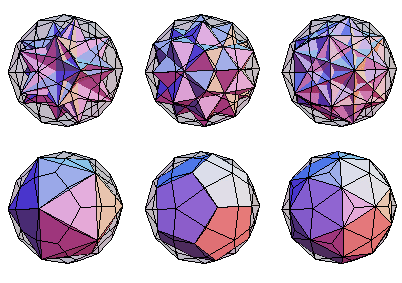
A tetrahedron 10-compound, octahedron 5-compound, cube 5-compound, icosahedron, dodecahedron, and icosidodecahedron can all be inscribed in the vertices of the deltoidal hexecontahedron (E. W. Weisstein, Dec. 24-27, 2009). The resulting compound of all these inscriptable solids is also illustrated above.
Starting from a small rhombicosidodecahedron of unit edge length, the edge lengths of the corresponding deltoidal hexecontahedron are
|
(1)
| |||
|
(2)
|
The corresponding midradius is
|
(3)
|
The surface area and volume are
|
(4)
| |||
|
(5)
|
