The Dedekind eta function is defined over the upper half-plane
by
|
(1)
| |||
 |
(2)
| ||
|
(3)
| |||
|
(4)
| |||
![q^_^(1/24){1+sum_(n=1)^(infty)(-1)^n[q^_^(n(3n-1)/2)+q^_^(n(3n+1)/2)]}](/images/equations/DedekindEtaFunction/Inline16.svg) |
(5)
| ||
|
(6)
|
(OEIS A010815), where is the square of the nome
,
is the half-period ratio,
and
is a q-series (Weber 1902, pp. 85 and 112;
Atkin and Morain 1993; Berndt 1994, p. 139).
The Dedekind eta function is implemented in the Wolfram Language as DedekindEta[tau].
Rewriting the definition in terms of explicitly in terms of the half-period
ratio
gives the product
 |
(7)
|
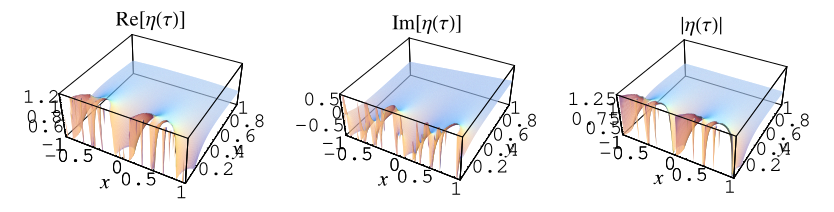
It is illustrated above in the complex plane.
is a modular form first introduced by Dedekind in
1877, and is related to the modular discriminant
of the Weierstrass elliptic function
by
|
(8)
|
(Apostol 1997, p. 47).
A compact closed form for the derivative is given by
|
(9)
|
where
is the Weierstrass zeta function and
and
are the invariants corresponding to the half-periods
. The derivative of
satisfies
|
(10)
|
where
is an Eisenstein series, and
|
(11)
|
A special value is given by
|
(12)
| |||
|
(13)
|
(OEIS A091343), where is the gamma function.
Another special case is
|
(14)
| |||
|
(15)
| |||
|
(16)
|
where
is the plastic constant,
denotes a polynomial
root, and
.
Letting
be a root of unity,
satisfies
|
(17)
| |||
|
(18)
| |||
|
(19)
|
where
is an integer (Weber 1902, p. 113; Atkin and Morain 1993; Apostol 1997, p. 47).
The Dedekind eta function is related to the Jacobi
theta function
by
 |
(20)
|
(Weber 1902, Vol. 3, p. 112) and
 |
(21)
|
(Apostol 1997, p. 91).
Macdonald (1972) has related most expansions of the form to affine root
systems. Exceptions not included in Macdonald's treatment include
, found by Hecke and Rogers,
, found by Ramanujan, and
, found by Atkin (Leininger and Milne 1999). Using the Dedekind
eta function, the Jacobi triple product identity
|
(22)
|
can be written
|
(23)
|
(Jacobi 1829, Hardy and Wright 1979, Hirschhorn 1999, Leininger and Milne 1999).
Dedekind's functional equation states that if , where
is the modular group
Gamma,
,
and
(where
is the upper half-plane), then
|
(24)
|
where
|
(25)
|
and
 |
(26)
|
is a Dedekind sum (Apostol 1997, pp. 52-57), with
the floor function.