MathWorld Headline News

The Mathematics of Tsunamis

By Eric W. Weisstein and Michael Trott

January 14, 2005--The recent tragic events following the December 2004 magnitude 9.0 earthquake in the Indian Ocean have reminded us of the need for scientific understanding and modeling of complicated physical phenomena in order to prevent unnecessary loss of life from natural disasters (cf. Post and Vatta 2005).

While the full-scale physics and modeling of tsunamis are difficult problems requiring the use of supercomputers and complicated custom software, a number of approximations can be made that render the problem of tsunami propagation tractable for a computer of modest power running off-the-shelf software such as Wolfram Research's Mathematica.

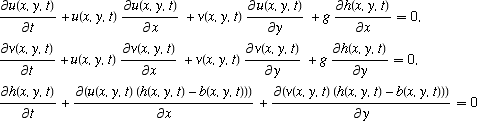
The simplest theory of water waves that reasonably approximates the behavior of real ocean waves is the system of coupled partial differential equations known as the shallow water wave equations (Pelinovsky et al. 2001, Layton 2002), reproduced above. Here, u and v are the horizontal velocity components of the water surface, x and y are the spatial coordinates of the wave, t is elapsed time, g is the acceleration due to gravity, and h is the height of the wave above the ocean floor topography b.

Part of the physics of tsunamis encompasses the phenomenon of "breaking," or flipping over, as waves near a coastline. However, as the top interface of the water touches only the layer of air above it, it is essentially free. This means the differential equations must be solved in the context of a so-called free boundary value problem, which in general are notoriously difficult to handle and require complicated and difficult computations (Guyenne and Grilli 2003). In addition, as a tsunami propagates over long distances, so-called Coriolis acceleration terms must be included to account for the fact that the frame of reference with respect to which the wave is propagating (i.e., the Earth) is rotating.

Zahibo et al. (2003) have carried out such full-blown calculations. But because the shallow water wave equations are difficult to solve, these equations are sometimes simplified in a number of ways, including by linearizing them. The linearized version takes the velocity of water particles to be (u, v) = , i.e., the gradient of a scalar potential. Even this linearized version has highly nontrivial boundary conditions that are difficult to treat correctly. Taking various asymptotic limits of Euler's equations of inviscid motion results in a host of integrable and nearly integrable equations such as the Korteweg-de Vries equation, Camassa-Holm equation, nonlinear Schrödinger equation, and so on (Rahman 1995, Johnson 2003). Unfortunately, while these equations have exact (integrable) solutions, they also diverge from the true behavior described by the full equations for any but very short time scales (Johnson 2003). Full solution of the shallow water wave equations is therefore needed in order to gain any realistic picture of tsunami propagation.

Visualization of a tsunami computed by Mathematica by numerically solving the shallow water wave equations. Initial conditions are a Gaussian displacement, and the bottom geometry is taken to be flat in the deep ocean, approaching the shoreline like a cosine function, and radially symmetric.

To create the tsunami visualization shown above, we used Mathematica's NDSolve command to solve the shallow water wave equations for an initial Gaussian water displacement. The ocean floor is assumed to be deep and of constant depth in the middle, while smoothly sloping towards the shore like a cosine function. In the animation above, we can clearly see a number of real physical effects, including (1) local propagation of the tsunami, (2) a small offset of the ocean level inside the radial wavefront (an effect only present in even-dimensional systems; in this case, 2-dimensional), and (3) a steepening of the wavefront as it nears the shore. The animation is halted as the wave nears the shore because the shallow wave equations cease providing an accurate description of the wave's propagation as the depth becomes comparable to the wavelength.

Much more complicated simulations performed with custom software and actual coastlines can be seen on the website of the National Oceanic and Atmospheric Administration. Readers interested in the code used to generate this animation may download the corresponding Mathematica notebook. Solving the equations takes less than a minute on a moderately fast desktop computer.