MathWorld Headline News

There Are No Magic Knight's Tours on the Chessboard

By Eric W. Weisstein

August 6, 2003--After 61.40 days of computation, a 150-year-old unsolved problem has finally been answered. The problem in question concerns the existence of a path that could be traversed by a knight on an empty numbered 8 x 8 chessboard.

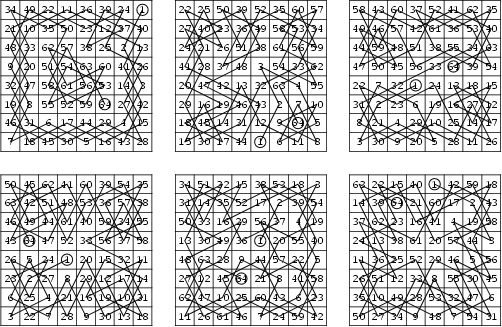
Recall that a knight is allowed to make L-shaped moves that offset its position by a single square in one direction and by two squares in a perpendicular direction. Now let a knight be allowed to move on an n x n chessboard whose squares are numbered from 1 to n² along the path of the knight, namely, the initial square is labeled "1," the second square it touches is labeled "2," and so on. This path is called a tour if it visits each square exactly once. The diagrams above illustrate six knight's tours on the 8 x 8 chessboard.

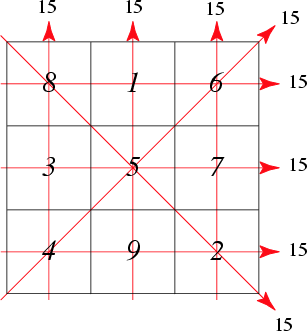
The array of numbers produced in a knight's tour can additionally satisfy a number of interesting properties. In particular, consider an array of numbers known as a magic square (or sometimes, a "diagonally magic square"), one of which is illustrated above. An n x n array of the numbers 1 to n² is called magic if the numbers in each row, column, and diagonal sum to a single number known as the magic constant of the square. For example, in the figure above, the magic constant is 15. A square that fails to be fully magic only because its diagonals fail to sum to the magic constant (but its rows and columns do sum to the magic constant) is then known as a semimagic square.

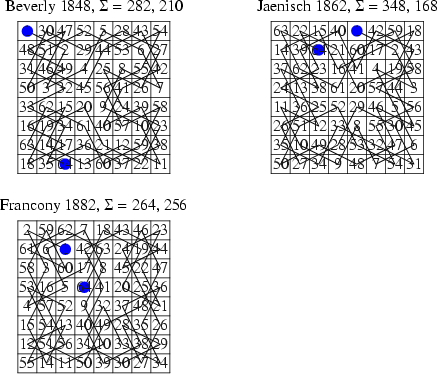
Not surprisingly, a knight's tour is called a magic tour if the resulting arrangement of numbers forms a magic square, and a semimagic tour if the resulting arrangement of numbers is a semimagic square. It has long been known that magic knight's tours are not possible on n x n boards for n odd. It was also known that such tours are possible for all boards of size 4k x 4k for k > 2. However, while a number of semimagic knight's tours were known on the usual 8 x 8 chessboard, including those illustrated above, it was not known if any fully magic tours existed on the 8 x 8 board.

This longstanding open problem has now been settled in the negative by an exhaustive computer enumeration of all possibilities. The software for the computation was written by J. C. Meyrignac, and the website http://magictour.free.fr was established by Guenter Stertenbrink to distribute and collect results for all possible tours. After 61.40 CPU-days, corresponding to 138.25 days of computation at 1 GHz, the project was completed on August 5, 2003. What are the results? In addition to netting a total of 140 distinct semimagic knight's tours, the computation demonstrated for the first time that no 8 x 8 magic knight's tour is possible, thus finally laying this long-open problem to rest.