The Hénon-Heiles equation is a nonlinear nonintegrable Hamiltonian system with
|
(1)
| |||
|
(2)
|
where the potential energy function is defined by the polar equation
|
(3)
|
giving Cartesian potential
|
(4)
|
The total energy of the system is then given by
|
(5)
|
which is conserved during motion.
Integrating the above coupled ordinary differential equations from an arbitrary starting point with
and
gives the motion illustrated above.
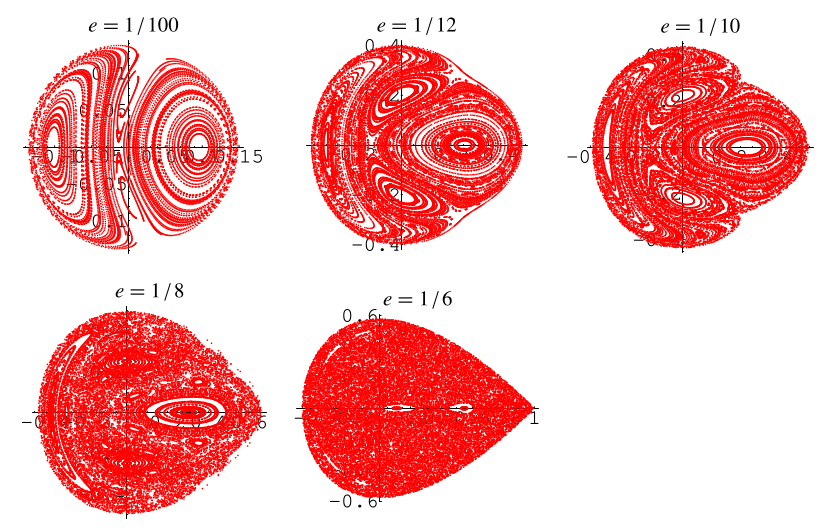
Surfaces of section are illustrated above for various initial energies ,
is plotted vs.
at values where
.
The Hamiltonian for a generalized Hénon-Heiles potential is
|
(6)
|
The equations of motion are integrable only for
1. ,
2. ,
3. ,
and
4. .
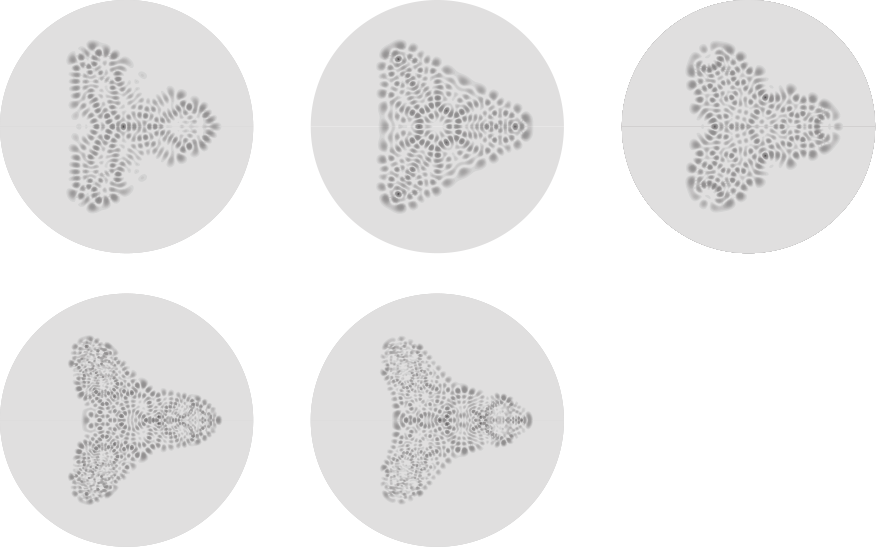
The plots above show a number of eigenfunctions of the Schrödinger equation with a generalized Hénon-Heiles potential
|
(7)
|
for certain specific values of (M. Trott, pers. comm., Jan. 6, 2004).