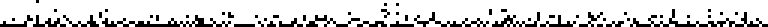
The continued fraction of is [1; 3, 1, 1, 5, 1, 1, 1, 3, 12, 4, 1, 271, 1, ...] (OEIS
A087501). A plot of the first 256 terms of
the continued fraction represented as a sequence of binary bits is shown above.
First occurrences of the terms 1, 2, 3, ... in the continued fraction occur at
, 15, 1, 10, 4, 19, 16, 77, 21, 62, 229, 9, 52, ... (OEIS
A225762). The smallest unknown value is 204,
which has
(E. Weisstein, Jul. 25, 2013).
The consecutively largest terms are 1, 3, 5, 12, 271, 12574, 13740, 78907, 133430, 574536, ... (OEIS A099791), occurring at positions 0, 1, 4, 9, 12, 266, 3170, 3212, 12961, 82527, ... (OEIS A225752).
Let the continued fraction of be denoted
and let the denominators of the convergents
be denoted
,
, ...,
. Then plots above show successive values of
,
,
, which appear to converge to Khinchin's
constant (left figure) and
, which appear to converge to the Lévy
constant (right figure), although neither of these limits has been rigorously
established.