The compact-open topology is a common topology used on function spaces. Suppose and
are topological spaces
and
is the set of continuous maps from
. The compact-open topology on
is generated by subsets of the following form,
|
(1)
|
where
is compact in
and
is open in
.
(Hence the terminology "compact-open.") It is important to note that these
sets are not closed under intersection, and do not form
a topological basis. Instead, the sets
form a subbasis
for the compact-open topology. That is, the open sets
in the compact-open topology are the arbitrary unions of finite intersections of
.
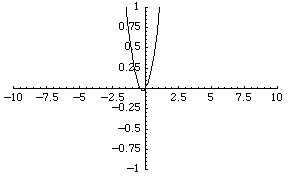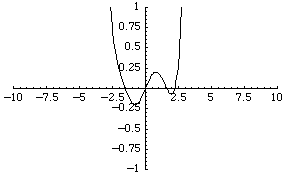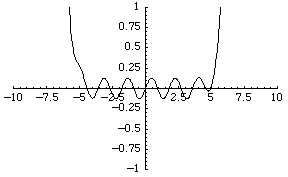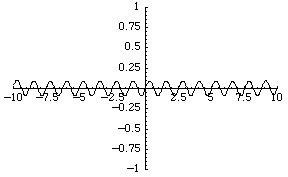
The simplest function space to compare topologies is the space of real-valued continuous functions . A sequence of functions
converges to
iff for every
containing
contains all but a finite number of the
. Hence, for all
and all
, there exists an
such that for all
,
|
(2)
|
For example, the sequence of functions converges to the zero
function, although each function is unbounded.
When
is a metric space, the compact-open topology is the
same as the topology of compact convergence. If
is a locally compact T2-space, a fairly weak condition, then the evaluation
map
|
(3)
|
defined by
is continuous. Similarly,
is continuous iff the map
, given by
, is continuous.
Hence, the compact-open topology is the right topology to use in homotopy
theory.