Clean tile is a game investigated by Buffon (1777) in which players bet on the number of different tiles a thrown coin will partially cover on a floor that is regularly tiled. Buffon investigated the probabilities on a triangular grid, square grid, hexagonal grid, and grid composed of rhombi. Assume that the side length of the tile is greater than the coin diameter . Then, on a square grid, it is possible for a coin to land so that it partially covers 1, 2, 3, or 4 tiles. On a triangular grid, it can land on 1, 2, 3, 4, or 6 tiles. On a hexagonal grid, it can land on 1, 2, or 3 tiles.

Special cases of this game give the Buffon-Laplace needle problem (for a square grid) and Buffon's needle problem (for infinite equally spaced parallel lines).

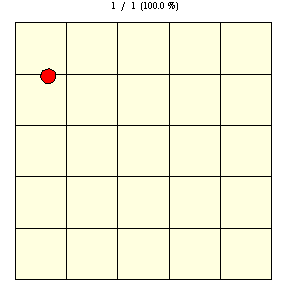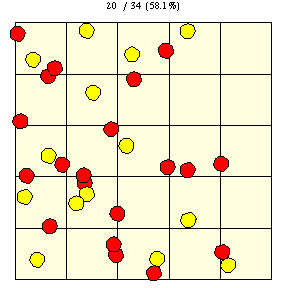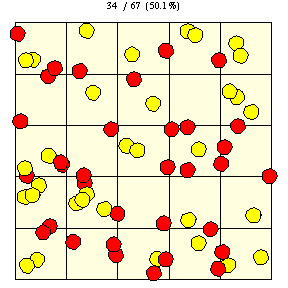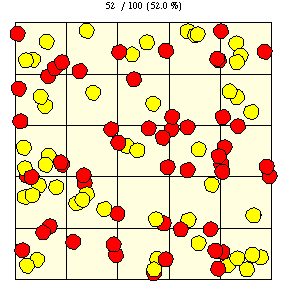
As shown in the figure above, on a square grid with tile edge length , the probability that a coin of diameter will lie entirely on a single tile (indicated by yellow disks in the figure) is given by

(1)

since the shortening of the side of a square obtained by insetting from a square of side length by the radius of the coin is given by

(2)

The probability that it will lie on two or more (indicated by red disks) is just

(3)

For the game to be fair with two players betting on (1) a single tile or (2) two or more tiles, these quantities must be equal, which gives

(4)

The probability of landing on exactly two tiles is the ratio of shaded area in the above figure to the tile size, namely

			(5)
			(6)

On a square grid, the probability of a coin landing on exactly three tiles is the fraction of a tile covered by the region illustrated in the figure above,

(7)

Similarly, the probability of a coin landing on four tiles is the fraction of a tile covered by a disk, as illustrated in the figure above,

(8)

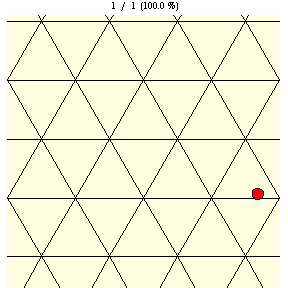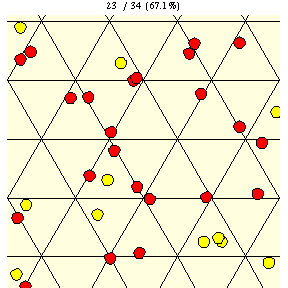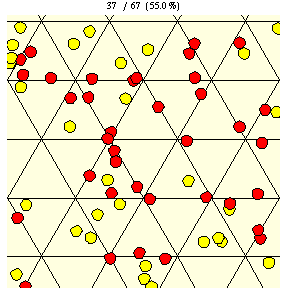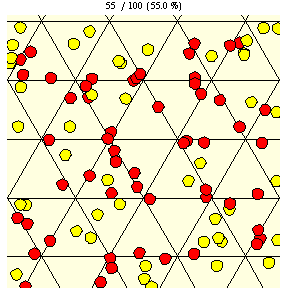
As shown in the figure above, on a triangular grid with tile edge length , the probability that a coin of diameter will lie entirely on a single tile is given by

(9)

since the shortening of the side of an equilateral triangle obtained by insetting from a triangle of side length by the radius of the coin is

(10)

The probability that it will lie on two or more is just

(11)

For the game to be fair with two players betting on (1) a single tile or (2) two or more tiles, these quantities must be equal, which gives

(12)

As shown in the figure above, on a hexagonal grid with tile edge length , the probability that a coin of diameter will lie entirely on a single tile is given by

(13)

since the shortening of the side of a regular hexagon obtained by insetting from a triangle of side length by the radius of the coin is

(14)

The probability that it will lie on two or more is just

(15)

For the game to be fair with two players betting on (1) a single tile or (2) two or more tiles, these quantities must be equal, which gives

(16)

In a quadrilateral tiling formed by rhombi with opening angle , insetting from a rhombus of side length gives

			(17)
			(18)

so

(19)

Therefore, the probability that a coin will lie on a single tile is

			(20)
			(21)

The probability that it will lie on two or more is just

(22)

For the game to be fair with two players betting on (1) a single tile or (2) two or more tiles, these quantities must be equal, which gives

(23)

As expected, this reduces to the square case for .

Buffon, G. "Essai d'arithmétique morale." Histoire naturelle, générale er particulière, Supplément 4, 46-123, 1777.

Mathai, A. M. "The Clean Tile Problem." §1.1.1 in An Introduction to Geometrical Probability: Distributional Aspects with Applications. Taylor & Francis: pp. 2-5, 1999.

Solomon, H. Geometric Probability. Philadelphia, PA: SIAM, 1978.

CITE THIS AS:

Weisstein, Eric W. "Clean Tile Problem." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/CleanTileProblem.html