Four circles ,
,
, and
are tangent to a fifth circle
or a straight line iff
|
(1)
|
where
is the length of a common tangent to circles
and
(Johnson 1929, pp. 121-122). The following cases are
possible:
1. If all the s
are direct common tangents, then
has like contact with all the circles,
2. If the s
from one circle are transverse while the other three are direct, then this one circle
has contact with
unlike that of the other three,
3. If the given circles can be so paired that the common tangents to the circles of each pair are direct, while the other four are transverse, then the members of
each pair have like contact with
(Johnson 1929, p. 125).
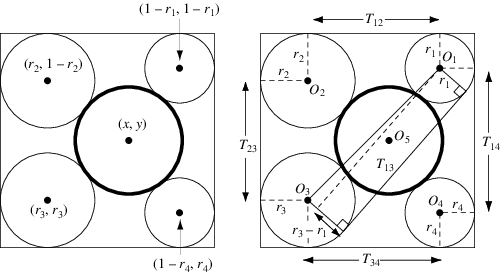
The special case of Casey's theorem shown above was given in a Sangaku problem from 1874 in the Gumma Prefecture. In this form, a single circle is drawn
inside a square, and four circles are then drawn around it, each of which is tangent
to the square on two of its sides. For a square of side length with lower left corner at
containing a central circle of radius
with center
, the radii and positions of the four circles can be found
by solving
|
(2)
|
|
(3)
|
|
(4)
|
|
(5)
|
Four of the
for the theorem are given immediately for the figure as
|
(6)
| |||
|
(7)
| |||
|
(8)
| |||
|
(9)
|
The remaining
and
can be found as shown in the above right figure. Let
be the distance from
to
, then
|
(10)
| |||
|
(11)
| |||
|
(12)
| |||
|
(13)
|
so
|
(14)
| |||
|
(15)
| |||
|
(16)
| |||
|
(17)
|
Since the four circles are all externally tangent to , the relevant form of Casey's theorem to use has signs
, so we have the equation
![(a-r_1-r_2)(a-r_3-r_4)+(a-r_1-r_4)(a-r_2-r_3)
-sqrt([2(a-r_1-r_3)^2-(r_3-r_1)^2][2(a-r_2-r_4)^2-(r_2-r_4)^2])=0](/images/equations/CaseysTheorem/NumberedEquation6.svg) |
(18)
|
(Rothman 1998). Solving for then gives the relationship
 |
(19)
|
Durell (1928) calls the following Casey's theorem: if is the length of a common tangent of two circles of radii
and
,
is the length of the corresponding common tangent of their inverses with respect
to any point, and
and
are the radii of their inverses, then
|
(20)
|